Bài tập 33 trang 91 SBT Toán 6 Tập 2
Bài tập 33 trang 91 SBT Toán 6 Tập 2
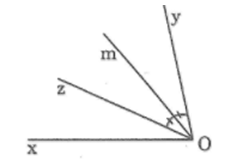
Cho hai tia Oy, Oz cùng nằm trong nửa mặt phẳng có bờ chứa tia Ox sao cho \(\widehat {xOy} = {80^0}\), \(\widehat {xOz} = {30^0}\). Gọi Om là tia phân giác của góc yOz. Tính \(\widehat {xOm}\)
Vì Oy và Oz cùng nằm trên một nửa mặt phẳng bờ chứa tia Ox, và \(\widehat {xOy} > \widehat {xOz}\)
nên tia Oz nằm giữa hai tia Ox; Oy
Suy ra:
\(\begin{array}{l}
\widehat {xOy} = \widehat {xOz} + \widehat {zOy}\\
\Rightarrow \widehat {zOy} = \widehat {xOy} - \widehat {xOz}\\
= {80^0} - {30^0} = {50^0}
\end{array}\)
Vì Om là tia phân giác của \(\widehat {yOz}\) nên:
\(\begin{array}{l}
\widehat {zOm} = \widehat {mOy}\\
= \frac{{\widehat {yOz}}}{2} = \frac{{{{50}^0}}}{2} = {25^0}
\end{array}\)
Vì Oz nằm giữa Ox và Om: nên \(\widehat {xOm} = \widehat {xOz} + \widehat {zOm}\)
Suy ra: \(\widehat {xOm} = {30^0} + {25^0} = {55^0}\)
-- Mod Toán 6
Copyright © 2021 HOCTAP247