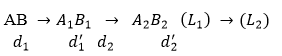Bài tập 3 trang 195 SGK Vật lý 11

Bài tập 3 trang 195 SGK Vật lý 11

Nhận định và phương pháp: 

Bài 3 là dạng bài Hệ hai thấu kính gồm 1 thấu kính và 1 thấu kính phân kỳ đồng trục ghép sát nhau.

Cách giải :

• Ta tiến hành giải theo các bước như sau:

  • Bước 1: Lập sơ đồ tạo ảnh qua hệ thấu kính

  • Bước 2: Xác định vị trí dựa vào sơ đồ tạo ảnh 

  • Bước 3: Tính số phóng đại ảnh cuối cùng cho bởi hệ hai thấu kính từ công thức \(k=\frac{\left | d'_2 \right |}{d_1}\)

  • Bước 4: Vẽ lại hình ảnh của hệ hai thấu kính đồng trục ghép sát nhau

  • Bước 5: Lặp lại tính toán và thay số vào theo yêu cầu của câu b.

Lời giải: 

Áp dụng phương pháp trên để giải bài 3 như sau: 

• Ta có: 

Câu a:

• Sơ đồ tạo ảnh qua hệ thấu kính:

• Ta có: \(d_1=20cm, f_1=20cm, l=30cm\)

⇒ \(d_1'=\propto\)

\(d_2=l-d_1'=-\propto\)

⇒ \(d_2'=f_2=-10cm\)

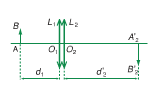
1. Vẽ hình 30.2 SGK: 

• Từ hình vẽ ta thấy: 

  • Vì \(A_1B_1\)  ở vô cực nên chùm tia sáng từ AB tới qua tâm O1 sẽ qua \(A_1B_1\) và là chùm tia song song . Tương tự, chùm tia sáng từ \(A_1B_1\) tới qua tâm O2 sẽ qua \(A_2B_2\)  cùng là chùm tia song song.

⇒ Tam giác  \(ABO_1\)đồng dạng với tam giác \(A_2B_2O_2\) suy ra:

\(k=\frac{A_2B_2}{AB}=\frac{A_2O_2}{AO_1}=\frac{\left | d'_2 \right |}{d_1}= \frac{\left |-10 \right |}{20}=\frac{1}{2}\)

Câu b:

• Ảnh \(A_2B_2\) là ảnh ảo và bằng hai lần vật. Ta có:

\(\Rightarrow d'_1=\frac{d_1.f_1}{d_1-f_1}=20.\frac{d_1}{d_1-20}\)

\(d_2=1-d_1\Rightarrow d_2=30\)

\(=20.\frac{d_1}{d_1-20}=\frac{10(d_1-60)}{d_1-20}\)

\(\Rightarrow \frac{5(60-d_1)}{d_1-40}< 0\)

\(\Rightarrow d_1<40 \ cm\) và \(d_2>60 \ cm\)

• Ảnh \(A_2B_2\) là ảnh ảo và bằng hai lần vật AB:

\(k=\left ( -\frac{d_1}{d_1} \right ).\left ( -\frac{d_2}{d_2} \right )= \frac{d_1.d_2}{d_1.d_2}\)

\(=\frac{10}{d_1-40}=\pm 2\Rightarrow \Rightarrow k=\pm 2=\frac{20}{d_1-60}\)    (*)

• Giải phương trình (*) ra ta được: \(d_1\)=35cm ( nhận) và \(d_1\) =45cm (loại)

Đáp số:

a. \(d_2'=f_2=-10cm\) và \(k=\frac{1}{2}\)

b. \(d_1\)=35cm 

-- Mod Vật Lý 11

Video hướng dẫn giải bài 3 SGK