Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 1. Tổng ba góc của một tam giác
Bài 8 trang 109 SGK Toán 7 tập 1
Bài 8 trang 109 SGK Toán 7 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác \(ABC\) có \(\widehat{B}=\widehat{C}= 40^0\). Gọi \(Ax\) là tia phân giác của góc ngoài ở đỉnh \(A\), Hãy chứng tỏ \(Ax// BC\).
Hướng dẫn giải
Áp dụng tính chất góc ngoài của một tam giác.
Áp dụng dấu hiệu nhận biết hai đường thẳng song song.
Lời giải chi tiết
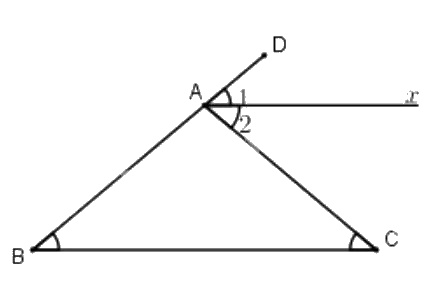
\(\widehat{CAD }\) = \(\widehat{B}\)+ \(\widehat{C}\) (góc ngoài của tam giác \(ABC\))
\(= 40^0\)+ \(40^0\) = \(80^0\)
\(\widehat{A_{2} }= \frac{1}2\widehat{CAD}=\frac{80}2=40^0\)
\(A_2=\widehat{BCA }\) hai góc ở vị trí so le trong bằng nhau nên \(Ax// BC\)
Copyright © 2021 HOCTAP247
