Bài 63 trang 136 SGK Toán 7 tập 1

Đề bài

Cho tam giác \(ABC\) cân tại\( A\). Kẻ \(AH\) vuông góc với \(BC\) ( \(H \) thuộc \(BC\)). Chứng minh rằng:

a) \( HB = HC\);

b) \(\widehat{BAH}=\widehat{CAH}\)

Hướng dẫn giải

a) Chứng minh ∆ABH = ∆ACH, suy ra \( HB = HC\)

b) Theo câu a), suy ra \(\widehat{BAH}=\widehat{CAH}\)

Lời giải chi tiết

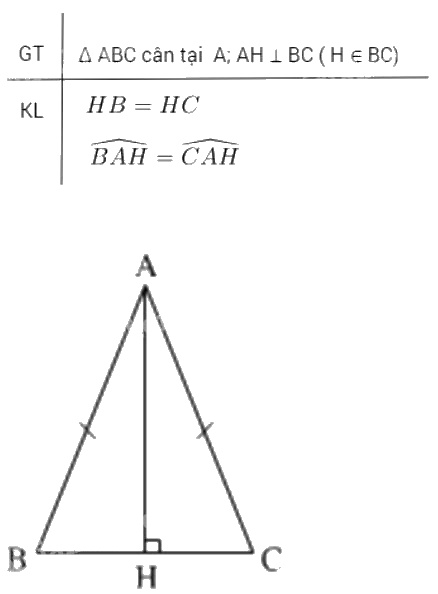
a) Tam giác \( ABH\) vuông tại \( H\)

Tam giác \(ACH\) vuông tai \(H\)

Xét hai tam giác vuông \(ABH\) và \( ACH\) có: 

+) \(AB = AC\) ( vì tam giác \(ABC\) cân tại \(A \))

+) \(AH\) cạnh chung.

Suy ra \(\Delta ABH = \Delta ACH\) (Cạnh huyền-cạnh góc vuông)

Suy ra \(HB=HC\) ( Hai cạnh tương ứng).

b) \( \Delta ABH = \Delta ACH \)  (Câu a)

Suy ra \(\widehat{BAH}\)=\(\widehat{CAH}\) (Hai góc tương ứng)