Bài 65 trang 137 SGK Toán 7 tập 1
Tóm tắt bài
Đề bài
Các tam giác \( ABC\) cân tại \( A\) (\(\widehat{A}\)< \(90^o\)). Vẽ \(BH \perp A \) (\( H\) thuộc \(AC\)), \(CK\perp AB\) (\( K \) thuộc \(AB\))
a) Chứng minh rằng \( AH = AK.\)
b) Gọi \( I\) là giao điểm của \( BH\) và \( CK\). Chứng minh rằng tia\( AI \) là tia phân giác của góc \( A.\)
Hướng dẫn giải
a) Chứng minh \( \Delta ABH = \Delta ACK\) , suy ra \( AH = AK \)
b) Chứng minh \(\widehat{IAK}=\widehat{IAH}\)
Lời giải chi tiết
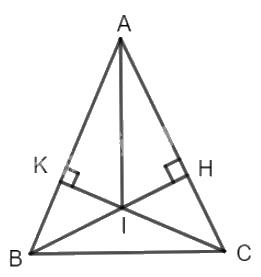
a) Hai tam giác vuông \(\Delta ABH \) và \(\Delta ACK\) có:
\(AB = AC\) (gt)
Góc \(A \) chung.
nên \( \Delta ABH = \Delta ACK\) (Cạnh huyền- Góc nhọn)
suy ra \(AH = AK.\)
b) Hai tam giác vuông \(AIK\) và \(AIH\) có:
\(AK = AH\) (cmt)
\(AI \) cạnh chung
Nên \( \Delta AIK = \Delta AIH\) (cạnh huyền- cạnh góc vuông)
Suy ra \(\widehat{IAK}\)=\(\widehat{IAH}\)
Vậy \(AI\) là tia phân giác của góc \(A\).
Copyright © 2021 HOCTAP247
