Giải bài 65 trang 137 - Sách giáo khoa Toán 7 tập 1

Đề bài

Cho ΔABC cân ở A. Vẽ BH vuông góc với AC, CK vuông góc với AB.

a) CMR AH = HK

b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A

Hướng dẫn giải

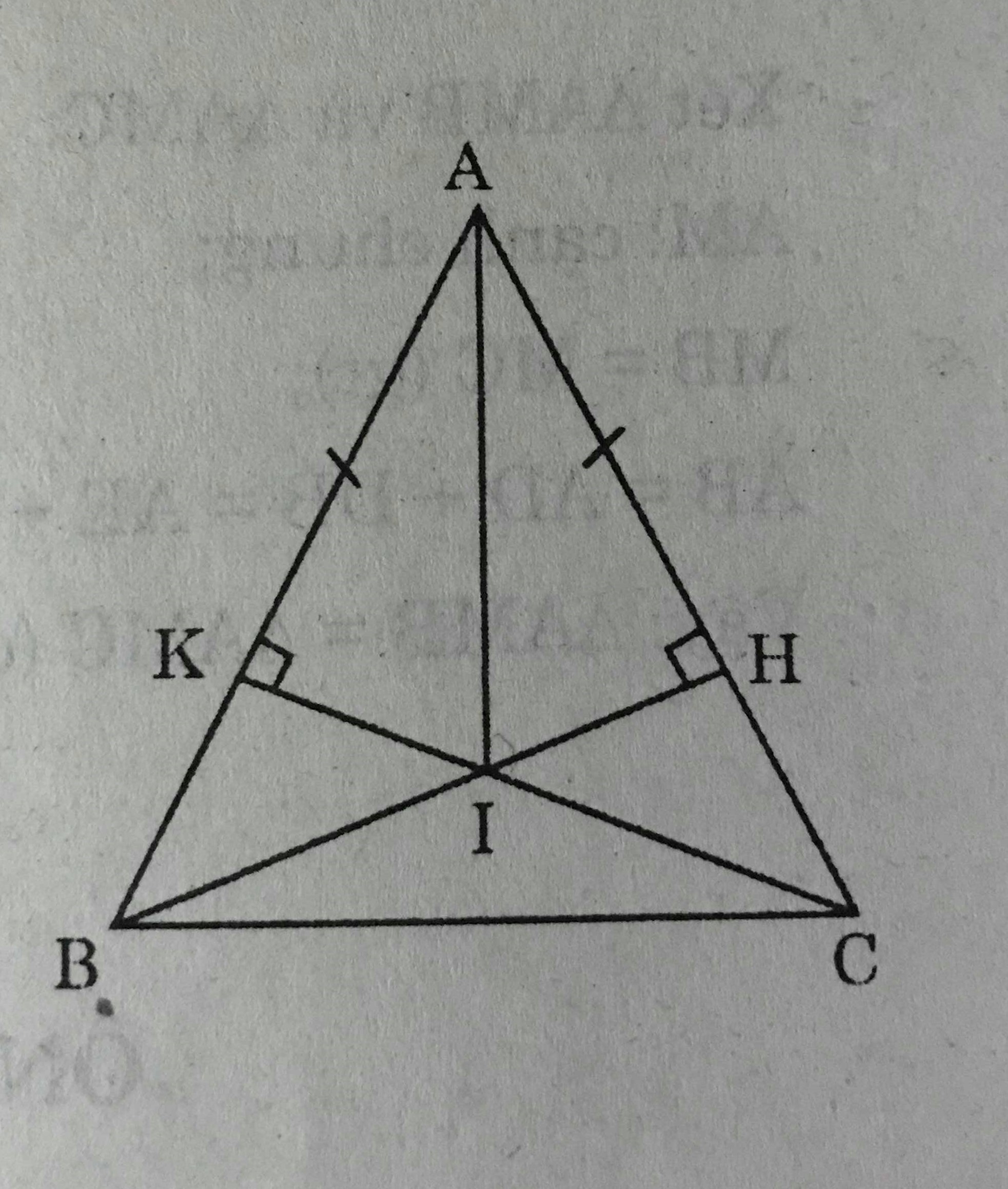
a) Xét  ΔABH và  ΔACK có :

\(\widehat{AKC}=\widehat{AHB}=90^0\)  ( \(AH \bot AC , CK \bot AB\))

AB = AC (hai cạnh bên của tam giác cân)

\(\widehat{A}\) là góc chung

Nên ΔABH = ΔACK (cạnh huyền - góc nhọn)

Suy ra : AH = AK (hai cạnh tương ứng của hai tam giác bằng nhau)

b) Xét ΔAIH và ΔAIK có :

AK = AH (câu a)

\(\widehat{K}=\widehat{H}=90^0\) (giả thiết)

AI là cạnh chung

Nên ΔAIH = ΔAIK (cạnh huyền - cạnh góc vuông)

Suy ra : \(\widehat{IAH}=\widehat{IAK}\) (hai góc tương ứng của hai tam giác bằng nhau)

=> AI là tia phân giác của góc A.