Đề kiểm tra 15 phút - Đề số 10 - Bài 7, 8 - Chương 2 - Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC.
a) Chứng minh \(\Delta AHB = \Delta AHC\)
b) Trên tia đối của tia BC lấy điểm D, trên tia đối của tia Cb lấy điểm E sao cho \(BD = CE\). Chứng minh rằng \(\Delta ADE\) cân.
Hướng dẫn giải
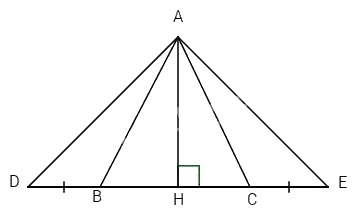
a) \(AH \bot BC\) (giả thiết).
Xét hai tam giác vuông AHB và AHC có :
+) AH cạnh chung,
+) \(AB = AC\) (giả thiết).
Do đó \(\Delta AHB = \Delta AHC\) (ch.cgv).
b) Ta có \(\widehat {ABD} + \widehat {ABC} = {180^o}\) (kề bù),
Tương tự \(\widehat {ACE} + \widehat {ACB} = {180^o}\) mà \(\widehat {ABC} = \widehat {ACB}\) (giả thiết)
\( \Rightarrow \widehat {ABD} = \widehat {ACE}\) (1).
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
+) \(AB = AC\) (giả thiết)
+) \( \widehat {ABD} = \widehat {ACE}\)
+) \(DB = CE\) (giả thiết).
Do đó \(\Delta ABD = \Delta ACE\) (c.g.c)
\( \Rightarrow AD = AE\) hay \(\Delta ADE\) cân.
Copyright © 2021 HOCTAP247
