Bài 46 trang 76 SGK Toán 7 tập 2

Đề bài

Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.

Hướng dẫn giải

Áp dụng định lí 2: Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.

Lời giải chi tiết

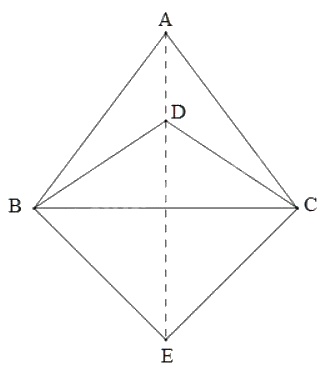
Vì ∆ABC cân tại A nên AB = AC

\( \Rightarrow\) A thuộc trung trực của BC (theo định lí 2)

Vì ∆DBC cân tại D nên DB = DC

\( \Rightarrow\) D thuộc trung trực của BC (theo định lí 2)

Vì ∆EBC cân tại E nên EB = EC

\( \Rightarrow\) E thuộc trung trực của BC (theo định lí 2)

Do đó A, D, E thuộc đường trung trực của BC.

Vậy A, D, E thẳng hàng.