Đề kiểm tra 15 phút - Đề số 1 - Bài 7 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC trung trực của cạnh AC cắt tia CB tại D (nằm ngoài đoạn BC). Trên tia đối của tia AD lấy E sao cho AE = BD. Chứng minh \(\Delta DCE\) cân.

Hướng dẫn giải

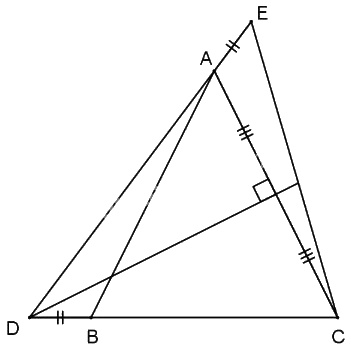
D thuộc trung trực của AC (gt) nên \(DA = DC.\)

\( \Rightarrow \Delta A{\rm{D}}C\) cân tại D.

Do đó \(\widehat {DAC} = \widehat {DCA} = \widehat {CBA}\) (gt)

\( \Rightarrow \widehat {DAC} = \widehat {CBA}\)

\(\widehat {E{\rm{A}}C} = \widehat {DBA}\) (kề bù với góc bằng nhau).

Vậy \(\Delta AB{\rm{D}} = \Delta CA{\rm{E}}\) (c.g.c)

\( \Rightarrow A{\rm{D}} = CE\) mà \(A{\rm{D}} = C{\rm{D}}\) (D thuộc trung trực của AC)

\( \Rightarrow CE = C{\rm{D}}\) hay \(\Delta DCE\) cân tại C.