Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 7. Tính chất đường trung trực của một đoạn thẳng
Bài 48 trang 77 SGK Toán 7 tập 2
Bài 48 trang 77 SGK Toán 7 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Hai điểm M và N cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng xy.
Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.
Hướng dẫn giải
Áp dụng tính chất đường trung trực của đoạn thẳng và bất đẳng thức tam giác.
Lời giải chi tiết
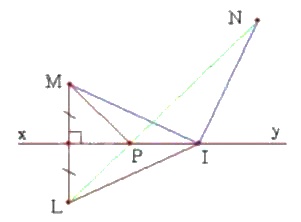
Gọi P là giao điểm của LN với xy.
- Nếu I không trùng P
Ta có: xy là đường trung trực của ML
\(\Rightarrow\) IM = IL (tính chất đường trung trực của đoạn thẳng)
Xét ΔINL có IL + IN > LN (bất đẳng thức tam giác)
\(\Rightarrow\) IM + IN > LN
- Nếu I ≡ P
IM + IN = IL + IN = LN
Vậy với mọi vị trí của I trên xy thì IL + IN ≥ LN.
Copyright © 2021 HOCTAP247
