Bài 3 trang 67 SGK Toán 8 tập 1

Đề bài

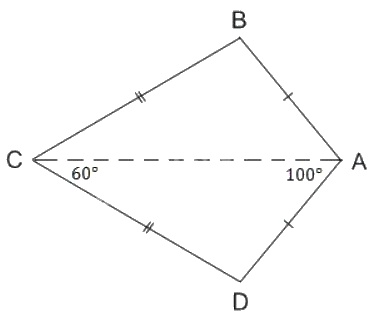
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều"

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính \(\widehat B;\widehat D\) biết rằng \(\widehat A = {100^0};\widehat C = {60^0}\).

Hướng dẫn giải

Áp dụng:

- Tính chất: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

- Định lý: Tổng 4 góc trong tứ giác bằng \({360^0}\)

- Tính chất hai tam giác bằng nhau.

Lời giải chi tiết

a) Ta có: AB = AD (gt)  => A thuộc đường trung trực của BD (Theo tính chất 1 điểm cách đều hai đầu của 1 đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó).

CB = CD (gt)   => C thuộc đường trung trực của BD (Theo tính chất 1 điểm cách đều hai đầu của 1 đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó).

Vậy AC là đường trung trực của BD.

b) Xét ∆ ABC và ∆ADC có:

  +) AB = AD (gt)

  +) BC = DC (gt)  

  +) AC cạnh chung

Suy ra ∆ ABC = ∆ADC (c.c.c)

Suy ra: \(\Rightarrow \widehat B = \widehat D\) (hai góc tương ứng)

Ta có: \(\widehat B + \widehat {BC{\rm{D}}} + \widehat {\rm{D}} + \widehat {BA{\rm{D}}} = {360^0}\)

\(\begin{array}{l}
\widehat B + \widehat {\rm{D}} = {360^0} - \left( {\widehat {BC{\rm{D}}} + \widehat {BA{\rm{D}}}} \right) \\\;\;\;\;\;\;\;\;\;\;\;= {360^0} - \left( {{{60}^0} + {{100}^0}} \right) = {200^0}\\
\Rightarrow \widehat B+\widehat B = {200^0} (\text{Vì }\widehat B= \widehat D)\\\Rightarrow 2\widehat B = 200^0
\end{array}\)

 Do đó \(\widehat B = \widehat {\rm{D}} = {200^0}:2 = {100^0}.\)