Giải bài 2 trang 66 - Sách giáo khoa Toán 8 tập 1
Tóm tắt bài
Đề bài
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác.
a) Tính các góc ngoài của tứ giác ở hình 7a.
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): \(\widehat{A_{1}}+\widehat{B_{1}}+\widehat{C_{1}}+\widehat{D_{1}}=?\)
c) Có nhận xét gì về tổng các góc ngoài của tứ giác ?
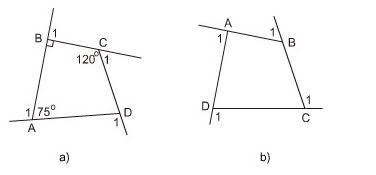
Hướng dẫn giải
a) Góc trong còn lại là :
\(\widehat{D}=360^{\circ}-90^{\circ}-120^{\circ}-75^{\circ}=75^{\circ}\)
Do đó \(\widehat{A}=180^{\circ}-75^{\circ}=105^{\circ}\) ; \(\widehat{B}=180^{\circ}-90^{\circ}=90^{\circ}\);
\(\widehat{B}=180^{\circ}-120^{\circ}=60^{\circ}\) ; \(\widehat{D}=180^{\circ}-75^{\circ}=105^{\circ}\);
b) Tổng các góc trong :
\(\widehat{A_{}}+\widehat{B_{}}+\widehat{C_{}}+\widehat{D_{}}=360^{\circ}\)
\(\widehat{A_{1}}+\widehat{B_{1}}+\widehat{C_{1}}+\widehat{D_{1}}\)
\(= (180^0 – \widehat{A}) + (180^0 – \widehat{B}) + (180^0 – \widehat{C}) + (180^0 – \widehat{D})\)
\(= 720 – (\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D}) = 720^0 – 360^0 = 360^0\)
c) Tổng các góc ngoài của tứ giác bằng 360^0
Copyright © 2021 HOCTAP247
