Bài 65 trang 100 SGK Toán 8 tập 1
Tóm tắt bài
Đề bài
Tứ giác \(ABCD\) có hai đường chéo vuông góc với nhau. Gọi \(E, F, G, H\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CD, DA\). Tứ giác \(EFGH\) là hình gì ? Vì sao ?
Hướng dẫn giải
Áp dụng: +) Tính chất đường trung bình của tam giác.
+) Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có một góc vuông là hình chữ nhật.
Lời giải chi tiết
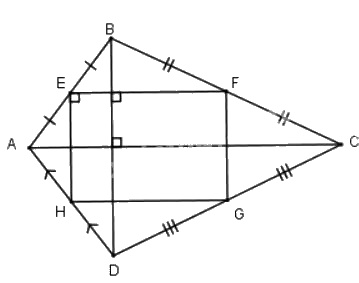
Vì \(E,F\) là trung điểm của \(AB,BC\)) (gt)
\( \Rightarrow \) \(EF\) là đường trung bình của \(∆ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(EF // AC\) (1) (tính chất đường trung bình của tam giác)
Do \(G,H\) là trung điểm của \(CD,DA) (gt)
\( \Rightarrow \) \( HG\) là đường trung bình của \(∆ADC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(HG // AC\) (2) (tính chất đường trung bình của tam giác)
Từ (1) và (2) \( \Rightarrow \) \(EF // HG\).
Vì \(E,H\) là trung điểm của \(AB,AD\)) (gt)
\( \Rightarrow \) \(EH\) là đường trung bình của \(∆ABD\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(EH // BD\) (3) (tính chất đường trung bình của tam giác)
Do \(G,F\) là trung điểm của \(CD,BC) (gt)
\( \Rightarrow \) \( GF\) là đường trung bình của \(∆BDC\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow \) \(GF // BD\) (4) (tính chất đường trung bình của tam giác)
Từ (3) và (4) \( \Rightarrow \) \(GF // EH\).
\( \Rightarrow \) \(EFGH\) là hình bình hành (dấu hiệu nhận biết hình bình hành)
Ta có: \(EF // AC\) và \(EH//BD\) mà \(AC\bot BD\) nên \(EF\bot EH\)
Hay \(\widehat{FEH} = 90^0\)
Hình bình hành \(EFGH\) có \(\widehat{E} = 90^0\) nên là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật).
Copyright © 2021 HOCTAP247
