Giải bài 75 trang 106 - Sách giáo khoa Toán 8 tập 1

Đề bài

Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.

Hướng dẫn giải

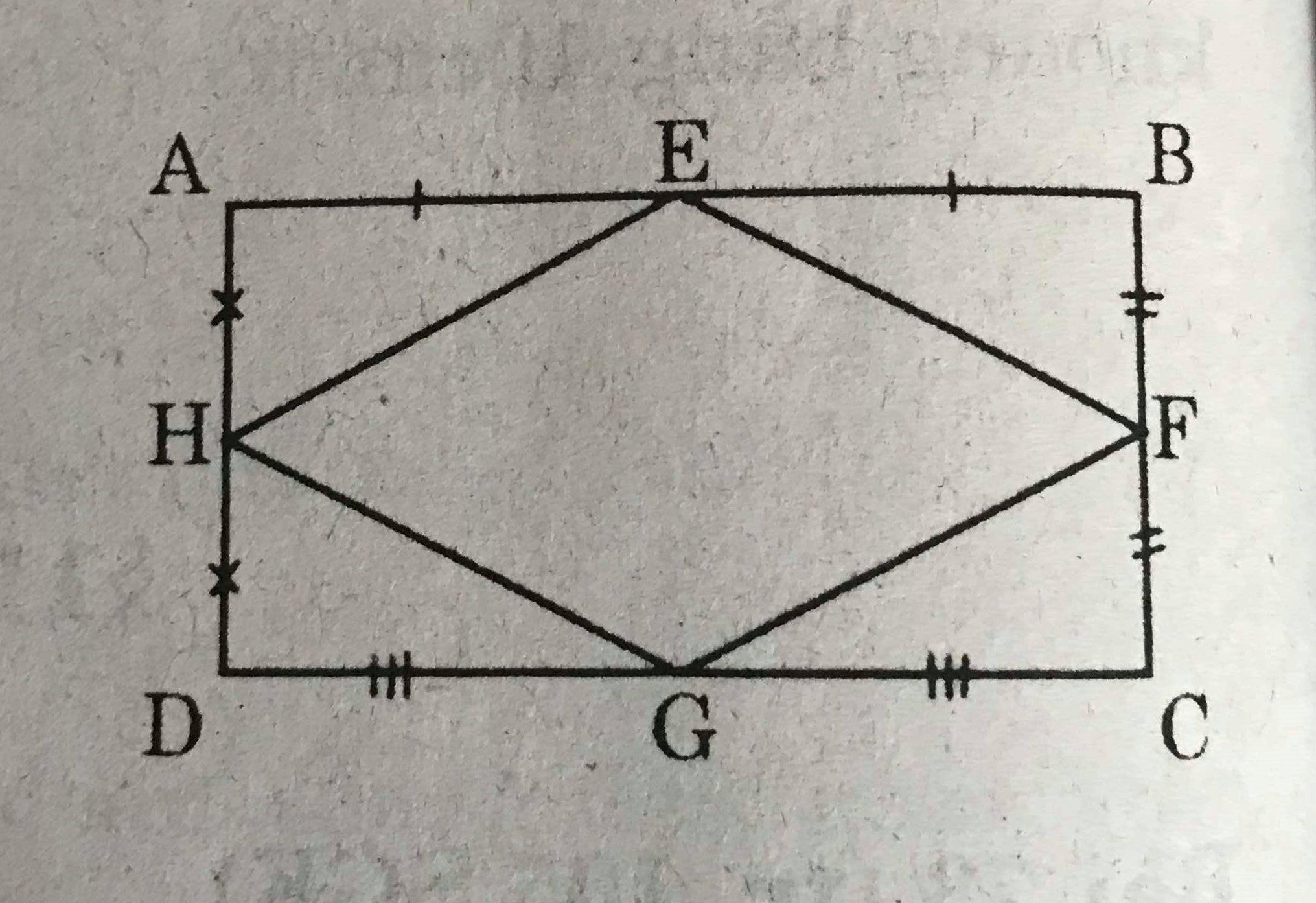
Xét \(\triangle\)AEH và \(\triangle\)BEF có :

EA = EB ( E là trung điểm của AB)

AH = BF (cùng bằng một nửa hai cạnh bằng nhau AD và BC).

\(\widehat{A}=\widehat{B}(=90^0)\)

Nên \(\triangle\)AEH = \(\triangle\)BEF (c.g.c) => EH = EF

Chứng minh tương tự : GH = GF , HE = HG.

Suy ra : EH = EF = GF = GH.

Do đó : EFGH là hình thoi.