Đề kiểm tra 15 phút - Đề số 3 - Bài 4 - Chương 1 - Hình học 9

Đề bài

Cho ∆ABC nhọn.

a. Chứng minh rằng : \(\sin A + \cos A > 1\)

b. Kẻ đường cao AH của tam giác ABC. Biết \(\widehat B = 60^\circ ,\,\widehat C = 45^\circ ,\) đường cao \(AH = 6cm\). Tính \({S_{ABC}}\)

Hướng dẫn giải

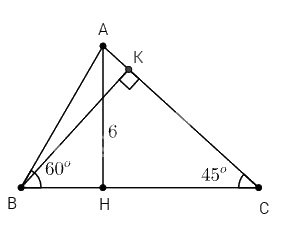
a. Kẻ đường cao BK, khi đó ∆AKB vuông tại K.

\(\eqalign{  & \sin A = {{BK} \over {AB}};\,\cos A = {{AK} \over {AB}}  \cr  &  \Rightarrow \sin A + \cos A = {{BK + AK} \over {AB}} > 1 \cr} \)

(bất đẳng thức tam giác)

b. Ta có: ∆AHC vuông cân nên \(HC = AH = 6\;(cm)\)

\(∆AHB\) vuông tại H có \(\widehat B = 60^\circ \) nên:

\(BH = AH.\cot 60^\circ  = 6.\cot 60^\circ  \)\(\,= 2\sqrt 3 \,\left( {cm} \right)\)  

Do đó: \(BC = BH + HC = 2\sqrt 3  + 6 \)\(\,= 2\left( {\sqrt 3  + 3} \right)\,\left( {cm} \right)\)

Vậy : \({S_{ABC}} = {1 \over 2}BC.AH \)\(\,= {1 \over 2}.2\left( {\sqrt 3  + 3} \right).6 \)\(\,= 6\left( {\sqrt 3  + 3} \right)\,\left( {c{m^2}} \right)\)