Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 1 - Hình học 9
Tóm tắt bài
Đề bài
Bài 1. Tính \(A = {\cos ^2}55^\circ - \cot 58^\circ + {{\tan 52^\circ } \over {\cot 38^\circ }}\)\(\, + {\cos ^2}35^\circ + \tan 32^\circ \)
Bài 2. Cho hình chữ nhật ABCD có đường chéo \(AC = 50cm\) và \(\widehat {BAC} = 30^\circ .\) Tính chu vi và diện tích hình chữ nhật.
Hướng dẫn giải
Bài 1. Ta có:
\({\cos ^2}35^\circ = {\sin ^2}55^\circ ;\cot 58^\circ = \tan 32^\circ ;\cot 38^\circ = \tan 52^\circ \)
Do đó:
\(\eqalign{ A &= {\cos ^2}55^\circ - \tan 32^\circ + {{\tan 52^\circ } \over {\tan 52^\circ }} + {\sin ^2}55^\circ + \tan 32^\circ \cr & = {\cos ^2}55^\circ + {\sin ^2}55^\circ + {{\tan 52^\circ } \over {\tan 52^\circ }} \cr&= 1 + 1 = 2 \cr} \)
Bài 2.
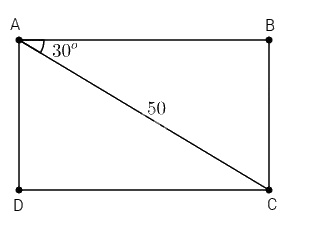
\(∆ABC\) vuông tại B có \(\widehat {BAC} = 30^\circ \) và \(AC = 50cm\) nên:
\(\eqalign{ & BC = AC.\sin 30^\circ \cr&\;\;\;\;\;\;\;= 50.\sin 30^\circ = 25\,\left( {cm} \right) \cr & AB = AC.\cos 30^\circ \cr&\;\;\;\;\;\;\; = 50.cos30^\circ = 25\sqrt 3 \,\left( {cm} \right) \cr} \)
Vậy chu vi hình chữ nhật ABCD là:
\(2(AB+BC) = 2\left( {25\sqrt 3 + 25} \right) \)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= 50\left( {\sqrt 3 + 1} \right)\,\left( {cm} \right) \)
\( {S_{ABCD}} = AB.BC = 25\sqrt 3 .25 \)\(\;= 625\sqrt 3 \,\left( {c{m^2}} \right) \)
Copyright © 2021 HOCTAP247
