Giải bài 6 trang 38 - Sách giáo khoa Toán 9 tập 2

Đề bài

    Cho hàm số y = f(x) = x2.

 a) Vẽ đồ thị của hàm số đó.

 b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).

 c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2.

 d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số  \(\sqrt{3};\sqrt{7}\)..

Hướng dẫn giải

      a) Lập bảng giá trị tương ứng của x, y và vẽ đồ thị:

  

x	-2	-1	0	1	2
\(y = x^2\)	4	1	0	1	4

 

 

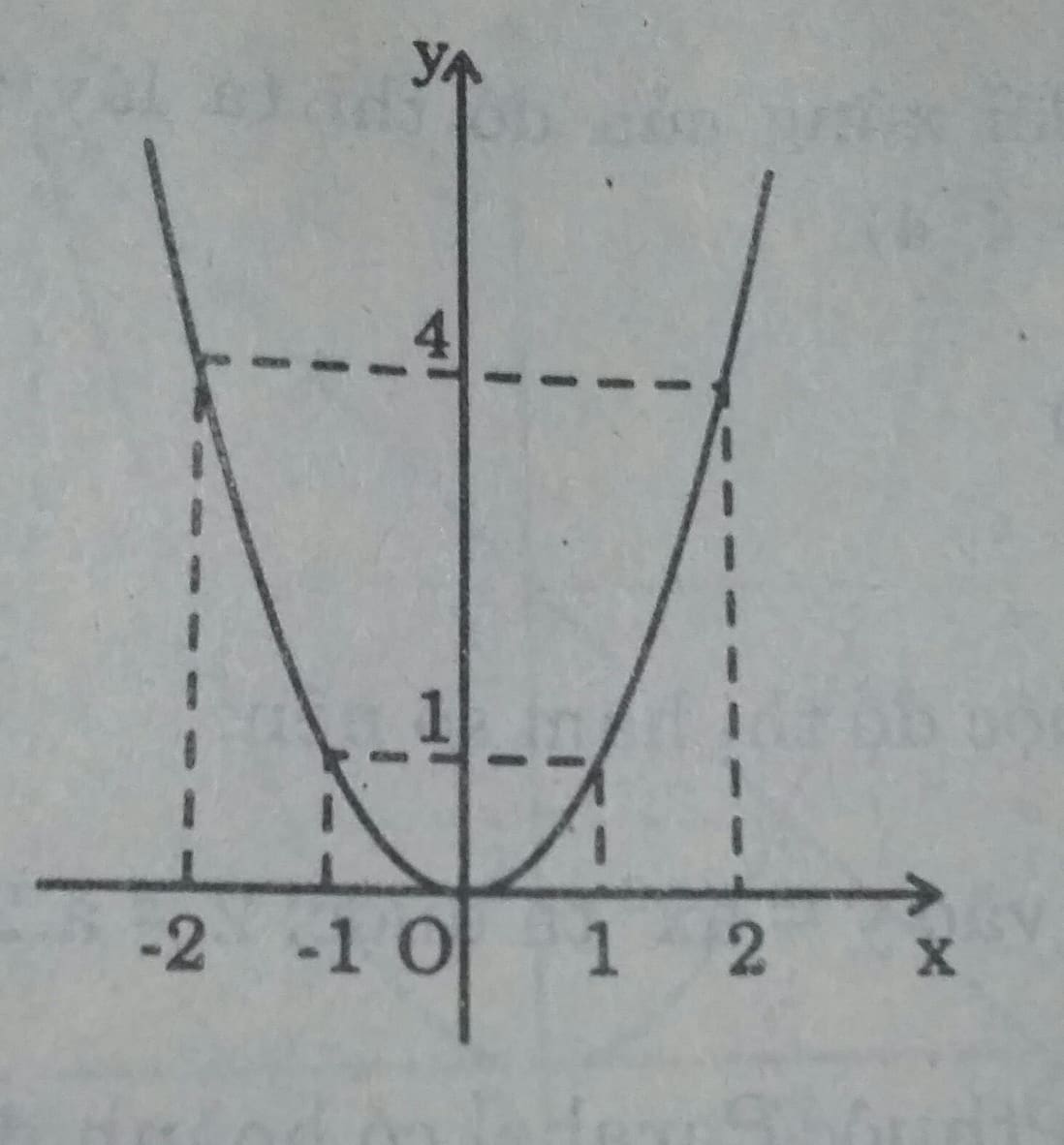
   b) Tính giá trị

   

	f(-8)	f(-1,3)	f(-0,75)	F(1,5)
x	-8	-1,3	-0,75	1,5
\(y = f(x) = x^2\)	64	1,69	0,5625	2,25

   c) Trên trục hoành ta lần lượt lấy các điểm có hoành độ là 0,5;1,5; 1,2, chiếu song song với trục tung lên đồ thị ta được các điểm. Từ các điểm này, ta chiếu song song với trục hoành ta được các giá trị cần ước lượng.

   Theo đồ thị ta có: 

   \( (0.5)^2 \approx 0,25 \\ (- 1,5)^2 \approx 2,25 \\ ( 2,5)^2 \approx 6,25\)

   d) Theo đồ thị ta có: Điểm trên trục hoành \( \sqrt{3}\) thì có tung độ là \( y = (\sqrt{3})^2=3\). Từ tung độ 3 trên trục tung, ta chiếu song song với trục hoành lên đồ thị ta được một điểm. Từ điểm này, ta chiếu song song với trục tung ta được giá trị \( \sqrt{3}\) trên trục hoành gần bằng 1,7.

   Tương tự biểu diễn \( \sqrt{7}\) gần bằng 2,7.