Nắm trọn lý thuyết đầy đủ nhất về hàm số - Toán lớp 10
Tóm tắt bài
Cùng với đi vào tìm hiểu những lý thuyết căn bản về hàm số. Trong bài viết tổng hợp các kiến thức như hàm số là gì, tập giá trị của hàm số, hàm số chẵn - hàm số lẻ, đồ thị hàm số \(y = x^2\)...
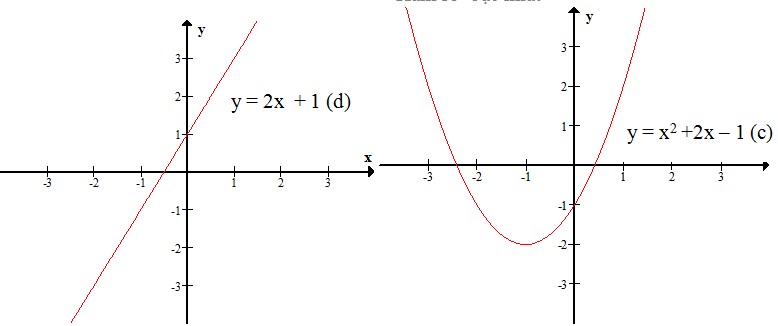
I) Hàm số
1) Khái niệm hàm số là gì?
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho mỗi giá trị của x ta luôn xác định một giá trị tương đương y thì y được gọi là hàm số của x.
2) Tính chất
- y được gọi là hàm hằng khi ta thay giá trị bất kì x vào y mà luôn nhận giá trị y không đổi.
- Hàm số có thể biểu diễn theo 2 cách, một là bằng bảng và hai là bằng công thức toán.
3) Các kí hiệu
- D được gọi là tập xác định (hay miền xác định của hàm số)
- x được gọi là biến cố.
- \(y_0 = f(x_0)\) tại \(x = x_0\)
Chú ý: Nếu bài toán cho hàm số bằng công thức mà không nêu rõ tập xác định thì ta hiểu ngầm tập xác định D là tập hợp các số \(x \in \mathbb{R}\).
4) Đồ thị
Đồng thị của hàm số là tập hợp các điểm (x,y) \(x\in D\) trên mặt phẳng tọa độ.
VD: Đồ thị hàm số \(y = x^2\)
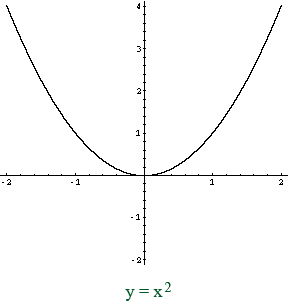
5) Tính chẵn lẻ
Cho hàm số f(x) có tập xác định \(D \in \mathbb{R}\)
- Hàm số y=f(x) được gọi là hàm số chẵn nếu \(x\in D \rightarrow -x \in D\) và \(f(-x)= f(x)\)
- Hàm số y=f(x) được gọi là hàm số lẻ nếu \(x\in D \rightarrow -x \in D\) và \(f(-x)= - f(x)\)
Đồ thị:
- Là trục tung với hàm số chẵn.
- Nhận gốc O của hệ trục tọa độ làm tâm đối xứng đối với hàm số lẻ.
II) Luyện tập
Bài 1: Tìm miền xác định của hàm số sau
a) \(y = f(x)= \sqrt{2-5x}\)
b) \(y = f(x)= \dfrac {\sqrt{x-2}}{x+1}\)
c) \(y = f(x)= \dfrac{x+5}{(x+1)\sqrt{x-1}}\)
d) \(y = f(x) = \dfrac {x+5}{x^3-5x+4}\)
e) \(y = f(x)=\dfrac {\sqrt{5-2x}}{(x-2)\sqrt{x-1}}\)
f) \(y = f(x) = \dfrac {x}{1-x^2}-\sqrt{-x}\)
g) \(y = f(x) = \dfrac {x+2}{\sqrt{x-1}-2}\)
Bài 2: Xét tính chẵn lẻ của các hàm số sau
a) \(y = x^4 - 4x^2 + 4\)
b) \(y = -2x^3 + 3x\)
c) \(y = (2x - 1)^2\)
d) \(y = x^2 + x+ 1\)
e) \(\dfrac {-x^2 + 1}{2x}\)
Xem thêm>>> Hướng dẫn bài tập SGK
Trên đây là bài viết mà đã tổng hợp được về hàm số, mong rằng bài viết sẽ hỗ trợ bạn hiểu được chính xác về tập giá trị của hàm số (miền giá trị của hàm số), hàm số chẵn là gì. Chúc các bạn học tập tốt <3
Copyright © 2021 HOCTAP247
