Bài 6 trang 18 SGK Đại số và Giải tích 11
Tóm tắt bài
Đề bài
Dựa vào đồ thị hàm số \(y = sinx\), tìm các khoảng giá trị của \(x\) để hàm số đó nhận giá trị dương.
Hướng dẫn giải
Tìm các khoảng chứa các điểm thuộc đồ thị hàm số \(y=sinx\) và nằm phía trên trục hoành trong khoảng \([-π ; π]\) và dựa vào chu kì tuần hoàn của đồ thị hàm số \(y=sinx\) suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía trên trục hoành.
Lời giải chi tiết
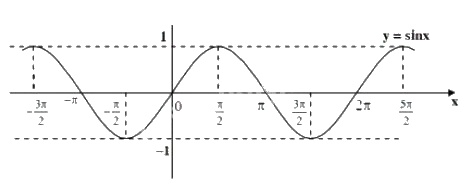
Nhìn đồ thị \(y = sinx\) ta thấy trong đoạn \([-π ; π]\) các điểm nằm phía trên trục hoành của đồ thị \(y = sinx\) là các điểm có hoành độ thuộc khoảng \((0 ; π)\).
Hàm số \(y=sinx\) là hàm số tuần hoàn với chu kì \(2\pi\). Từ đó, tất cả các khoảng giá trị của \(x\) để hàm số đó nhận giá trị dương là \((0 + k2π ; π + k2π)\) hay \((k2π ; π + k2π)\) với \(k \in Z\).
Copyright © 2021 HOCTAP247
