Bài 7 trang 18 SGK Đại số và Giải tích 11
Tóm tắt bài
Đề bài
Dựa vào đồ thị hàm số \(y = cos x\), tìm các khoảng giá trị của \(x\) để hàm số đó nhận giá trị âm.
Hướng dẫn giải
Tìm các khoảng chứa các điểm thuộc đồ thị hàm số \(y=cosx\) và nằm phía dưới trục hoành trong khoảng \([0 ; 2π]\) và dựa vào chu kì tuần hoàn của đồ thị hàm số \(y=cosx\) suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía dưới trục hoành.
Lời giải chi tiết
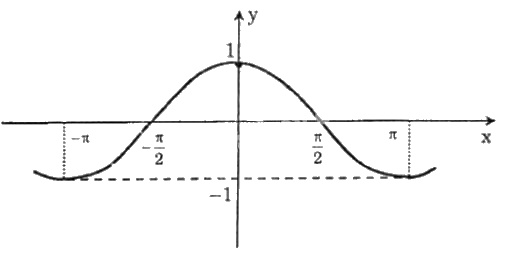
Xét trên khoảng \([0 ; 2π]\), dựa vào đồ thị hàm số \(y = cosx\), để làm hàm số nhận giá trị âm thì: \(\left( {{\pi \over 2};{{3\pi } \over 2}} \right)\)
Do hàm số \(y=cosx\) tuần hoàn với chu kì \(2 \pi\) nên tất cả các khoảng mà đồ thị hàm số nằm phía dưới trục hoành là \(x \in \left( {{\pi \over 2} + k2\pi ;{{3\pi } \over 2} + k2\pi } \right),k \in Z\)
Copyright © 2021 HOCTAP247
