Bài 1 trang 29 SGK Hình học 11

Đề bài

Cho tam giác \(ABC\) có ba góc nhọn và \(H\) là trực tâm. Tìm ảnh của tam giác \(ABC\) qua phép vị tự tâm \(H\), tỉ số \( \frac{1}{2}\)

Hướng dẫn giải

Sử dụng khái niệm phép vị tự: Phép vị tự tâm I tỉ số k biến M thành điểm M' \( \Rightarrow \overrightarrow {IM'}  = k\overrightarrow {IM} \).

Lời giải chi tiết

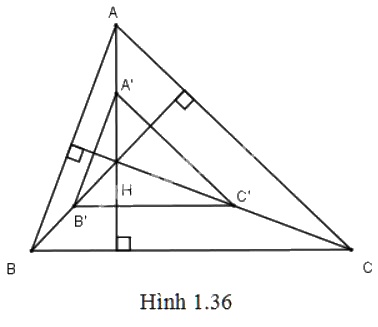
Ta có: \(\overrightarrow {HA'}  = \frac{1}{2}\overrightarrow {HA} ;\,\,\overrightarrow {HB'}  = \frac{1}{2}\overrightarrow {HB} ;\,\,\overrightarrow {HC'}  = \frac{1}{2}\overrightarrow {HC} \)

Vậy ảnh của \(A, B, C\) lần lượt là trung điểm \(A', B', C'\) của các cạnh \(HA, HB, HC\)