Bài 2 trang 29 SGK Hình học 11

Đề bài

Tìm tâm vị tự của hai đường tròn trong các trường hợp sau

Hướng dẫn giải

Dựa vào định nghĩa phép vị tự.

Lời giải chi tiết

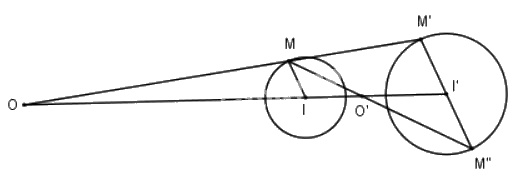
Lấy điểm \(M\) thuộc đường tròn \((I)\). Qua \(I'\) kẻ đường thẳng song song với \(IM\), đường thẳng này cắt đường tròn \((I')\) tại \(M'\) và \(M''\). Hai đường thẳng \(MM'\) và \(MM''\) cắt đường thẳng \(II'\) theo thứ tự \(O\) và \(O'\). Khi đó, \(O\) và \(O'\) là các tâm vị tự cần tìm

Vì hai đường tròn đã cho có bán kính khác nhau nên chúng có hai tâm vị tự là \(O\) và \(O'\), xác định trong từng trường hợp như sau ( xem hình vẽ):

a) Trường hợp 1: Hai đường tròn không cắt nhau

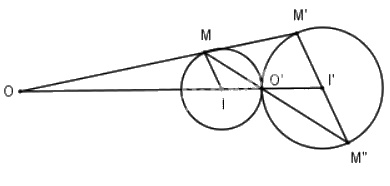
b) Trường hợp 2: Hai đường tròn tiếp xúc nhau.

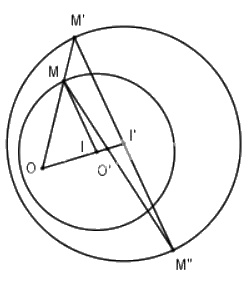
c) Trường hợp 3: Hai đường tròn chứa nhau.