Phép vị tự - Những lý thuyết cần ghi nhớ

PHÉP VỊ TỰ - NHỮNG LÝ THUYẾT CẦN GHI NHỚ

Phép vị tự là kiến thức quan trọng mà các em học sinh cần nắm được trong bộ môn Toán 11. .com soạn ra bài viết dưới đây nhằm giúp các em nắm được toàn bộ thông tin cần thiết. 

I. Phép vị tự là gì?

Phép VT tâm O tỉ số k là phép biến hình, biến mỗi điểm M thành điểm M' sao cho 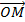 = k .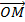

Ký hiệu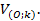 

II. Tính chất phép vị tự 

- Phép VT tâm O tỉ số k biến 2 điểm M, N thành M', N' thì 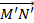 = k.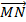

Đoạn M'N' = \(| k |\)MN.

- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi thứ tự các điểm ấy. 

- Biến một đường thẳng thành đường thẳng song song hoặc trùng với nó (nếu tâm vị tự O \(\epsilon \Delta \)hoặc tỉ số k = 1 thì \( \Delta \)' trùng với \(\Delta \)).

- Biến một tia thành một tia. 

- Biến một đoạn thẳng thành đoạn thẳng có độ dài gấp \(| k |\).

- Biến một tam giác thành một tam giác đồng dạng. 

- Biến một góc thành một góc bằng nó. 

- Biến đường tròn bán kính R thành đường tròn bán kính R' = \(| k.R |\).

III. Biểu thức tọa độ 

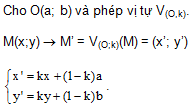
Đặc biệt: Nếu O(0;0) thì \(\binom{x' = k.x}{y' = k.y}\) 

IV. Phép vị tự đường tròn 

Định lý: Với hai đường tròn bất kỳ luôn có một phép VT biến đường tròn này thành đường tròn kia. Tâm phép này được gọi là tâm VT của hai đường tròn. 

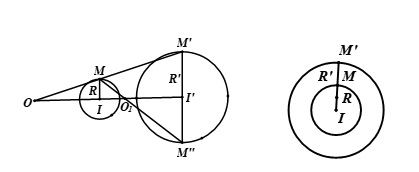
Cho hai đường tròn (I; R) và (I', R')

- Nếu I \(\equiv \) I' thì các phép VT V\(_{(I; \pm \frac{R'}{R})}\) biến (I; R) thành (I'; R').

- Nếu I \(\neq\) I' và R \(\neq\)R' thì các phép VT V\(_{(O; \frac{R'}{R})}\)và V\(_{(O_{1}; \frac{R'}{R})}\) biến (I; R) thành (I', R'). Ta gọi O là tâm VT ngoài còn O\(_{1}\) là tâm VT trong của hai đường tròn.

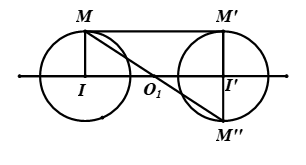
- Nếu I \(\neq\) I' và R = R' thì V\(_({O_{1}; -1})\) biến (I; R) thành (I', R').

Trên đây là toàn bộ lý thuyết mà các em đã, đang và sẽ được học. Rất mong đem lại cho quý độc giả những thông tin bổ ích. Sau khi học xong, độc giả có thể tham khảo các bài tập về phép vị tự.