Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 9. Độ dài đường tròn, cung tròn
Giải bài 68 trang 95 - Sách giáo khoa Toán 9 tập 2
Giải bài 68 trang 95 - Sách giáo khoa Toán 9 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho ba điểm A, B, C thẳng hàng sao cho B nằm giữa A và C. Chứng minh rằng độ dài của nửa đường tròn đường kính AC bằng tổng các độ dài của hai nửa đường tròn đường kính AB và BC.
Hướng dẫn giải
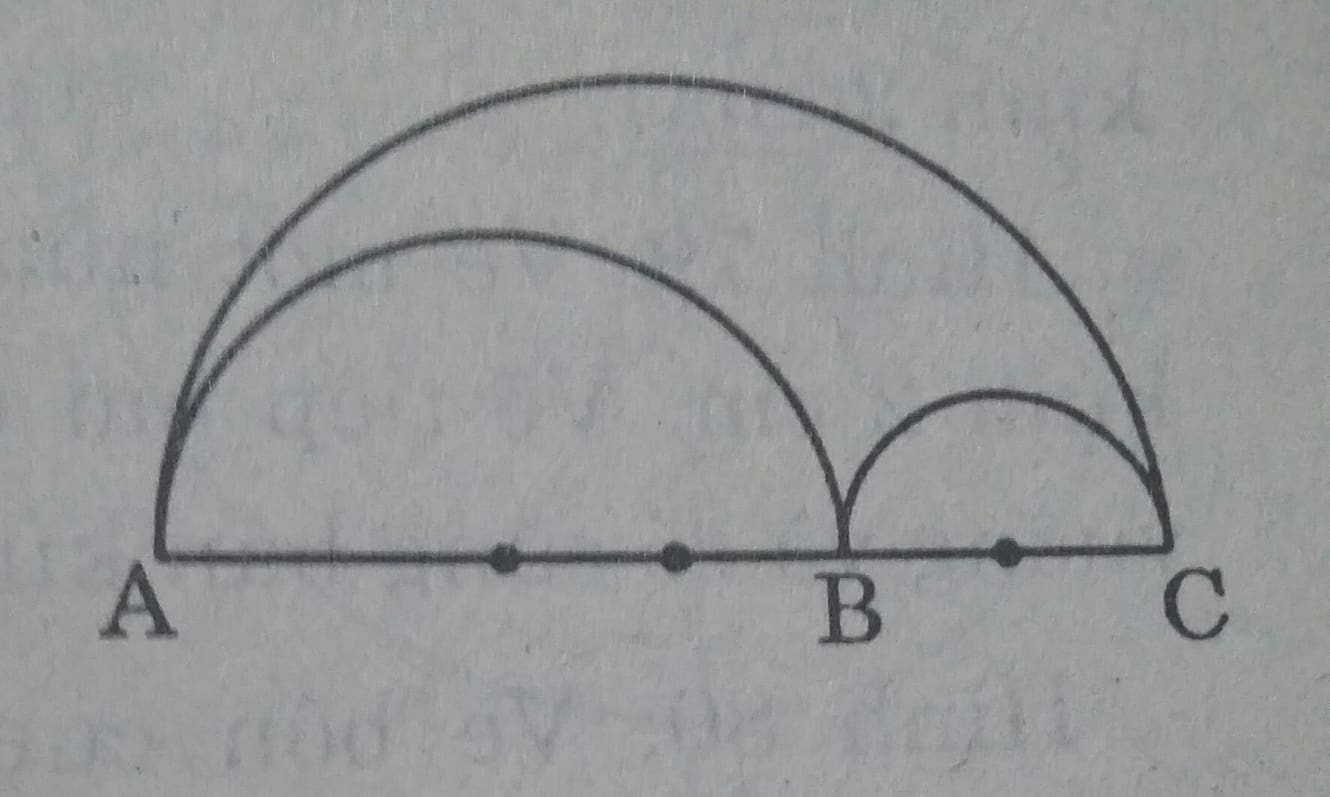
Gọi \(C_1, C_2,C_3\) lần lượt là độ dài của các nửa đường tròn đường kính AC,AB,BC.
Ta có:
\(C_1= \pi\dfrac{R}{2};C_2= \pi\dfrac{AB}{2}; C_3=\pi \dfrac{BC}{2}\\ C_2+C_3 = \pi\dfrac{AB}{2}+\pi \dfrac{BC}{2}= \dfrac{\pi }{2}(AB+BC)= \pi .AC=C_1\\ Vậy \ C_1 = C_2+C_3\)
Copyright © 2021 HOCTAP247
