Mặt nón, khối nón !!
Câu 1 :
Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là
Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là
A.
B.
C.
D.
Câu 2 :
Công thức tính diện tích toàn phần hình nón có bán kính đáy r, độ dài đường cao h và độ dài đường sinh l là:
Công thức tính diện tích toàn phần hình nón có bán kính đáy r, độ dài đường cao h và độ dài đường sinh l là:
A.
B.
C.
D.
Câu 3 :
Công thức tính thể tích khối nón có bán kính đáy r, độ dài đường sinh l và chiều cao h là:
Công thức tính thể tích khối nón có bán kính đáy r, độ dài đường sinh l và chiều cao h là:
A.
B.
C.
D.
Câu 4 :
Công thức tính thể tích khối nón biết diện tích đáy Sd và đường sinh l là:
A.
B.
C.
D.
Câu 5 :
Diện tích xung quanh hình nón có bán kính đáy r = 3cm và độ dài đường sinh 4cm là:
Diện tích xung quanh hình nón có bán kính đáy r = 3cm và độ dài đường sinh 4cm là:
A.
B.
C.
D.
Câu 6 :
Cho hình nón có các kích thước r = 1cm; l = 2cm với r, l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
Cho hình nón có các kích thước r = 1cm; l = 2cm với r, l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
A.
B.
C.
D.
Câu 7 :
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng:
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng:
A.
B.
C.
D.
Câu 8 :
Cho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
Cho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
A.
B.
C.
D.
Câu 9 :
Cho hình nón đỉnh S có bán kính đáy R = 2. Biết diện tích xung quanh của hình nón là . Tính thể tích khối nón.
Cho hình nón đỉnh S có bán kính đáy R = 2. Biết diện tích xung quanh của hình nón là . Tính thể tích khối nón.
A.
B.
C.
D.
Câu 10 :
Cho hình nón có các kích thước r = 1; h = 2 với r,hr,h lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
Cho hình nón có các kích thước r = 1; h = 2 với r,hr,h lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
A.
B.
C.
D.
Câu 11 :
Thể tích khối nón có bán kính đáy r = 2cm và h = 3cm là:
A.
B.
C.
D.
Câu 12 :
Cho tam giác ABO vuông tại O, có góc Quay tam giác ABO quanh trục AO ta được một hình nón có diện tích xung quanh bằng:
Cho tam giác ABO vuông tại O, có góc Quay tam giác ABO quanh trục AO ta được một hình nón có diện tích xung quanh bằng:
A.
B.
C.
D.
Câu 13 :
Một hình nón tròn xoay có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng . Khi đó chiều cao h của hình nón bằng:
Một hình nón tròn xoay có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng . Khi đó chiều cao h của hình nón bằng:
A.
B.
C.
D.
Câu 14 :
Hình nón có thiết diện qua trục là tam giác đều cạnh a = 3 . Tính độ dài đường cao của hình nón.
Hình nón có thiết diện qua trục là tam giác đều cạnh a = 3 . Tính độ dài đường cao của hình nón.
A.3
B.
C.
D.
Câu 15 :
Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là thỏa mãn
Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là thỏa mãn
A.
B.
C.
D.
Câu 17 :
Cho hình nón có diện tích xung quanh bằng và bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho.
Cho hình nón có diện tích xung quanh bằng và bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho.
A.
B.
C.
D. l = 3a .
Câu 19 :
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là 1350. Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí M để diện tích SAM đạt giá trị lớn nhất
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là 1350. Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí M để diện tích SAM đạt giá trị lớn nhất
A.Vô số
B.3
C.2
Câu 22 :
Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
A.
B.
C.
D.
Câu 23 :
Cho tam giác ABC đều, có diện tích bằng s1 và AH là đường cao. Quay tam giác ABC quanh đường thẳng AH ta thu được hình nón có diện tích xung quanh bằng s2. Tính .
Cho tam giác ABC đều, có diện tích bằng s1 và AH là đường cao. Quay tam giác ABC quanh đường thẳng AH ta thu được hình nón có diện tích xung quanh bằng s2. Tính .
A.
B.
C.
D.
Câu 24 :
Một cái phễu có dạng hình nón có chiều cao 15(cm). Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn).
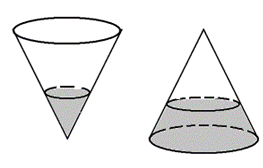
Một cái phễu có dạng hình nón có chiều cao 15(cm). Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn).

A.0,577(cm)
B.0,216(cm)
C.0,325(cm)
Câu 27 :
Cho hình nón N1 có chiều cao bằng 40cm. Người ta cắt hình nón N1 bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ N2 có thể tích bằng 18 thể tích N1. Tính chiều cao h của hình nón N2?
Cho hình nón N1 có chiều cao bằng 40cm. Người ta cắt hình nón N1 bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ N2 có thể tích bằng 18 thể tích N1. Tính chiều cao h của hình nón N2?
A.20cm.
B.10cm.
C.5cm
Câu 28 :
Một hình nón đỉnh S có bán kính đáy bằng , góc ở đỉnh là 1200. Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất Smax của thiết diện đó là bao nhiêu?
Một hình nón đỉnh S có bán kính đáy bằng , góc ở đỉnh là 1200. Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất Smax của thiết diện đó là bao nhiêu?
A.
B.
C.
D.
Câu 29 :
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính tan góc giữa hai mặt phẳng (BCC′B′) và (ABCD).
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính tan góc giữa hai mặt phẳng (BCC′B′) và (ABCD).
A.
B.
C.
D.
Câu 30 :
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính thể tích khối tứ diện ACB′D′.
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính thể tích khối tứ diện ACB′D′.
A.
B.
C.
D.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247