Cho đường tròn (O), điểm M nằm ngoài đường tròn (O). kẻ hai tiếp tuyến MB, MC (B và C là các tiếp điểm) với đường tròn. Trên
Câu hỏi :
Cho đường tròn (O), điểm M nằm ngoài đường tròn (O). kẻ hai tiếp tuyến MB, MC (B và C là các tiếp điểm) với đường tròn. Trên cung lớn BC lấy điểm A sao cho AB < AC. Từ điểm M kẻ đường thẳng song song với AB, đường thẳng này cắt đường tròn (O) tại D và E (MD < ME),cắt BC tại F, cắt AC tại I.
a) Chứng minh tứ giác MBOC nội tiếp.
b) Chứng minh \(FD.FE = FB.FC;FI > FE = FD.FE\)
c) Đường thẳng OI cắt đường tròn (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt đường tròn (O) tại K (K khác Q). Chứng minh 3 điểm P, K, M thẳng hàng.
Cho đường tròn (O), điểm M nằm ngoài đường tròn (O). kẻ hai tiếp tuyến MB, MC (B và C là các tiếp điểm) với đường tròn. Trên cung lớn BC lấy điểm A sao cho AB < AC. Từ điểm M kẻ đường thẳng song song với AB, đường thẳng này cắt đường tròn (O) tại D và E (MD < ME),cắt BC tại F, cắt AC tại I.
a) Chứng minh tứ giác MBOC nội tiếp.
b) Chứng minh \(FD.FE = FB.FC;FI > FE = FD.FE\)
c) Đường thẳng OI cắt đường tròn (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt đường tròn (O) tại K (K khác Q). Chứng minh 3 điểm P, K, M thẳng hàng.
* Đáp án
* Hướng dẫn giải
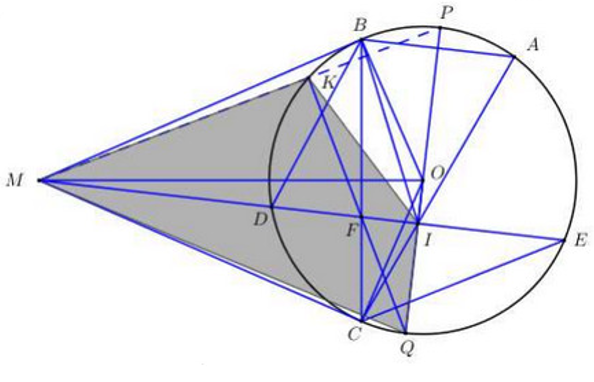
a) Do MB, MC là hai tiếp tuyến của đường tròn (O) nên \(\widehat {OBM} = \widehat {OCM} = {90^0}\)
Xét tứ giác MBOC có: \(\widehat {OBM} + \widehat {OCM} = {180^0}\) suy ra tứ giác MBOC là tứ giác nội tiếp.
b) Xét tam giác FBD và tam giác FEC có:
\(\widehat {BFD} = \widehat {EFC}\left( {dd} \right)\)
\(\widehat {FDB} = \widehat {FCE}\) ( hai góc nội tiếp cùng chắn cung BE)
\( \Rightarrow \Delta FBD \sim \Delta FEC\left( {g - g} \right) \Rightarrow \frac{{FB}}{{FE}} = \frac{{FD}}{{FC}} \Rightarrow FD.FE = FB.FC\left( 1 \right)\)
Ta có AB// ME suy ra \(\widehat {BAC} = \widehat {DIC}\)
Mà \(\widehat {BAC} = \widehat {MBC}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BC)
\( \Rightarrow \widehat {DIC} = \widehat {MBC} \Rightarrow \widehat {MBF} = \widehat {CIF}\)
Xét tam giác FBM và tam giác FIC có:
\(\widehat {BFM} = \widehat {IFC}\) (đđ)
\(\widehat {MBF} = \widehat {CIF}\left( {cmt} \right)\)
\( \Rightarrow \Delta FBM \sim \Delta FIC\left( {g - g} \right) \Rightarrow \frac{{FB}}{{FI}} = \frac{{FM}}{{FC}} \Rightarrow FI.FM = FB.FC\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow FI.FM = FD.FE\left( 3 \right)\)
c) Xét tam giác FDK và tam giác FQE có:
\(\widehat {KFD} = \widehat {EFQ}\) (đđ)
\(\widehat {FKD} = \widehat {FEQ}\)( hai góc nội tiếp cùng chắn cung DQ)
\( \Rightarrow \Delta FKD \sim \Delta FEQ\left( {g - g} \right)\)
\( \Rightarrow \frac{{FK}}{{FE}} = \frac{{FD}}{{FQ}} \Rightarrow FD.FE = FK.FQ\left( 4 \right)\)
Từ (3) và (4) \( \Rightarrow FI.FM = FK.FQ \Leftrightarrow \frac{{FM}}{{FQ}} = \frac{{FK}}{{FI}}\)
Xét tam giác FMQ và tam giác FKI có:
\(\frac{{FM}}{{FQ}} = \frac{{FK}}{{FI}}\left( {cmt} \right)\)
\(\widehat {MFQ} = \widehat {KFI}\)
\( \Rightarrow \Delta FMQ \sim \Delta FKI\left( {c - g - c} \right) \Rightarrow \widehat {FMQ} = \widehat {FKI}\)
Suy ra tứ giác KIQM là tứ giác nội tiếp
\( \Rightarrow \widehat {MQK} = \widehat {MIQ}\)(hai góc nội tiếp cùng chắn cung MQ)
Ta có \(\widehat {MBF} = \widehat {CIF} \Rightarrow \widehat {MBC} = \widehat {MIF}\) suy ra tứ giác MBIC là tứ giác nội tiếp
Mà MOBC là tứ giác nội tiếp nên M, B, O, I, C cùng thuộc 1 đường tròn.
Ta có \(\widehat {OBM} = {90^0}\) suy ra OM là đường kính của đường tròn đi qua 5 điểm M, B, O, I, C.
Suy ra \(\widehat {OIM} = {90^0}\)(góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow IM \bot OI \Rightarrow \widehat {MIQ} = {90^0}\)
\( \Rightarrow \widehat {MKQ} = \widehat {MIQ} = {90^0}\)
Lại có \(\widehat {QKP} = {90^0}\)(góc nội tiếp chắn nửa đường tròn)
Từ đó ta có: \(\widehat {MKP} = \widehat {MKQ} + \widehat {QKP} = {180^0}\)
Vậy 3 điểm P, K, M thẳng hàng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
