1. Cho Parabol (P ) y = - x^2 và đường thẳng (d): y = x - 2 a) Vẽ ( P ) và (d) trên cùng một mặt phẳng tọa độ Oxy

1.

a) \(\left( P \right):\,\,y = - {x^2}\)

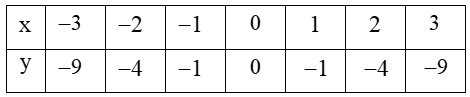
\(\left( d \right):\,\,y = x - 2\)

\(x = 0 \Rightarrow y = - 2:\,\,\,\,\,\,\left( {0; - 2} \right)\)

\(y = 0 \Rightarrow x = 2:\,\,\,\,\,\,\left( {2;0} \right)\)

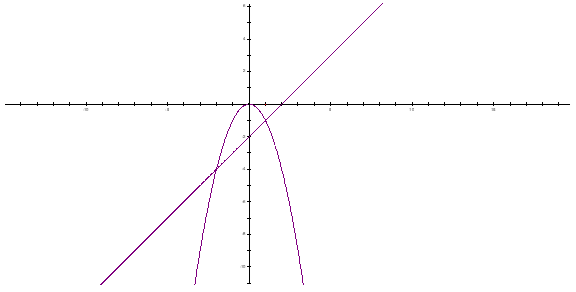
b) Phương trình đường thẳng \(\left( {d'} \right)\) có dạng \(y = {\rm{ax}} + b\)

 \(\left( {d'} \right)\)//\(\left( d \right):y = x - 2 \Rightarrow a = 1;\,\,b \ne - 2\)

Phương trình hoành độ giao điểm của \(\left( P \right)\,v{\rm{\`a }}\,\left( {d'} \right)\)là \( - {x^2} = x + b \Leftrightarrow {x^2} + x + b = 0\,\,\left( * \right)\)

PT \(\left( * \right)\) có \(\Delta = 1 - 4b\).

\(\left( P \right)\,v{\rm{\`a }}\,\left( {d'} \right)\)tiếp xúc nhau khi PT \(\left( * \right)\) có nghiệm kép \( \Leftrightarrow \Delta = 0 \Leftrightarrow 1 - 4b = 0 \Leftrightarrow b = \frac{1}{4}\) (nhận).

Vậy PT đường thẳng \(\left( {d'} \right)\,\,l{\rm{\`a }}:\,y = x + \frac{1}{4}\)

2.

a) PT \({x^2} - 4x + m = 0\)có một nghiệm bằng \( - 1\)\( \Rightarrow a - b + c = 0 \Rightarrow 1 + 4 + m = 0 \Rightarrow m = - 5\).

Nghiệm còn lại của PT là \( - \frac{c}{a} = - \frac{m}{1} = - \frac{{ - 5}}{1} = 5\)

b) ĐK \(\Delta ' = {\left( { - 2} \right)^2} - m \ge 0 \Leftrightarrow m \le 4\)

Áp dụng định lí Vi et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = m\end{array} \right.\)

\(\begin{array}{l}\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4 \Rightarrow 9{x_1}{x_2} + 3\left( {{x_1} + {x_2}} \right) + 1 = 4\\ \Rightarrow 9m + 3.4 + 1 = 4 \Rightarrow m = - 1\,\left( {tm} \right)\end{array}\)

Vậy \(m = - 1\) là giá trị cần tìm.