Cho đường tròn (O;R) có đường kính AB. Vẽ dây cung CD vuông góc với AB (CD không đi qua tâm O). Trên tia đối của tia BA

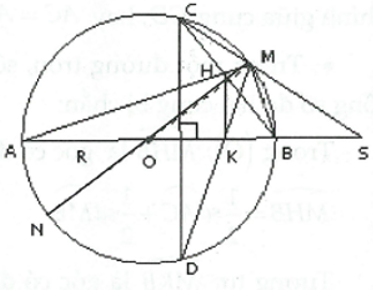
1) \(\Delta SBC\) và \(\Delta SMA\) có:

\(\widehat {BSC} = \widehat {MSA}\), \(\widehat {SCB} = \widehat {SAM}\) (góc nội tiếp cùng chắn )

\( \Rightarrow \Delta DBC\) đồng dạng với \(\Delta SMA\).

Nhận xét: Bài toán chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.

2) Vì \(AB \bot CD\) nên .

Suy ra: \(\widehat {MHB} = \widehat {MKB}\) (vì cùng bằng )

\( \Rightarrow \) Tứ giác BMHK nội tiếp được đường tròn \( \Rightarrow \widehat {HMB} + \widehat {HKB} = 180^\circ \). (1)

Lại có: \(\widehat {HMB} = \widehat {AMB} = 90^\circ \) (2) (góc nội tiếp chắn nửa đường tròn)

Từ (1) (2) suy ra \(\widehat {HKB} = 90^\circ \) do đó \(HK//CD\) (cùng vuông góc với AB).

Nhận xét: Bài toán chứng minh hai đường thẳng song song bằng cách chứng minh chúng cùng vuông góc với một đường thẳng thứ ba.

3) Vẽ đường kính MN suy ra  .

Ta có:

Mà  và  nên \(\widehat {OSM} = \widehat {OMK}\)

\( \Rightarrow \Delta OSM\) đồng dạng với \(\Delta OMK\)

\( \Rightarrow \frac{{OS}}{{OM}} = \frac{{OM}}{{OK}} \Rightarrow OK.OS = {R^2}\)

Nhận xét: Bài toán chứng minh một đẳng thức bằng cách chứng minh tam giác đồng dạng.