Cho tam giác ABC vuông ở A. Trên cạnh AC lấy 1 điểm M, dựng đường tròn tâm (O) có đường kính MC. Đường thẳng BM cắt đường

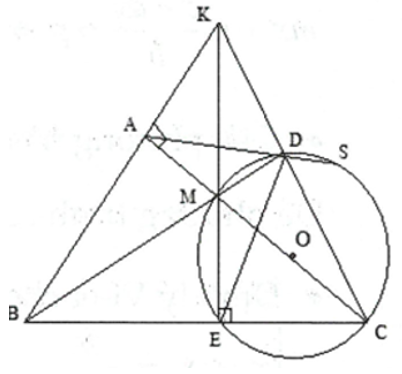
1) Ta có \[\widehat {BAC} = 90^\circ \left( {gt} \right)\]

\[\widehat {MDC} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn )

A, D nhìn BC dưới góc \[90^\circ \] , tứ giác ABCD nội tiếp

Vì tứ giác ABCD nội tiếp \[ \Rightarrow \widehat {ADB} = \widehat {ACB}\](cùng chắn cung AB) (1)

Ta có tứ giác DMCS nội tiếp \[ \Rightarrow \widehat {ADB} = \widehat {ACS}\](cùng bù với\[\widehat {MDS}\])    (2)

Từ (1) và (2) \[ \Rightarrow \widehat {BCA} = \widehat {ACS}\]

2) Giả sử BA cắt CD tại K. Ta có \[BD \bot CK,CA \bot BK\]

\[ \Rightarrow M\] là trực tâm \[\Delta KBC\]. Mặt khác \[\widehat {MEC} = 90^\circ \](góc nội tiếp chắn nửa đường tròn)

\[ \Rightarrow K,M,E\] thẳng hàng, hay BA, EM, CD đồng quy tại K

3) Vì tứ giác ABCD nội tiếp \[ \Rightarrow \widehat {DAC} = \widehat {DBC}\](cùng chắn )       (3)

Mặt khác tứ giác BAME nội tiếp \[ \Rightarrow \widehat {MAE} = \widehat {MBE}\](cùng chắn ) (4)

Từ (3) và (4) \[ \Rightarrow \widehat {DAM} = \widehat {MAE}\] hay AM là tia phân giác \[\widehat {DAE}\]

Chứng minh tương tự \[\widehat {ADM} = \widehat {MDE}\] hay DM là tia phân giác \[\widehat {ADE}\]

Vậy M là tâm đường tròn nội tiếp \[\Delta ADE\]