Cho tam giác ΔABC cân tại A, nội tiếp đưởng tròn (O). M là một điểm trên cung nhỏ AC (M ≠ A; C), MC cắt tia BA tại I. Tiếp tuyến tại B của đường tròn (O) cắt AM tại E. Gọi N là gia...

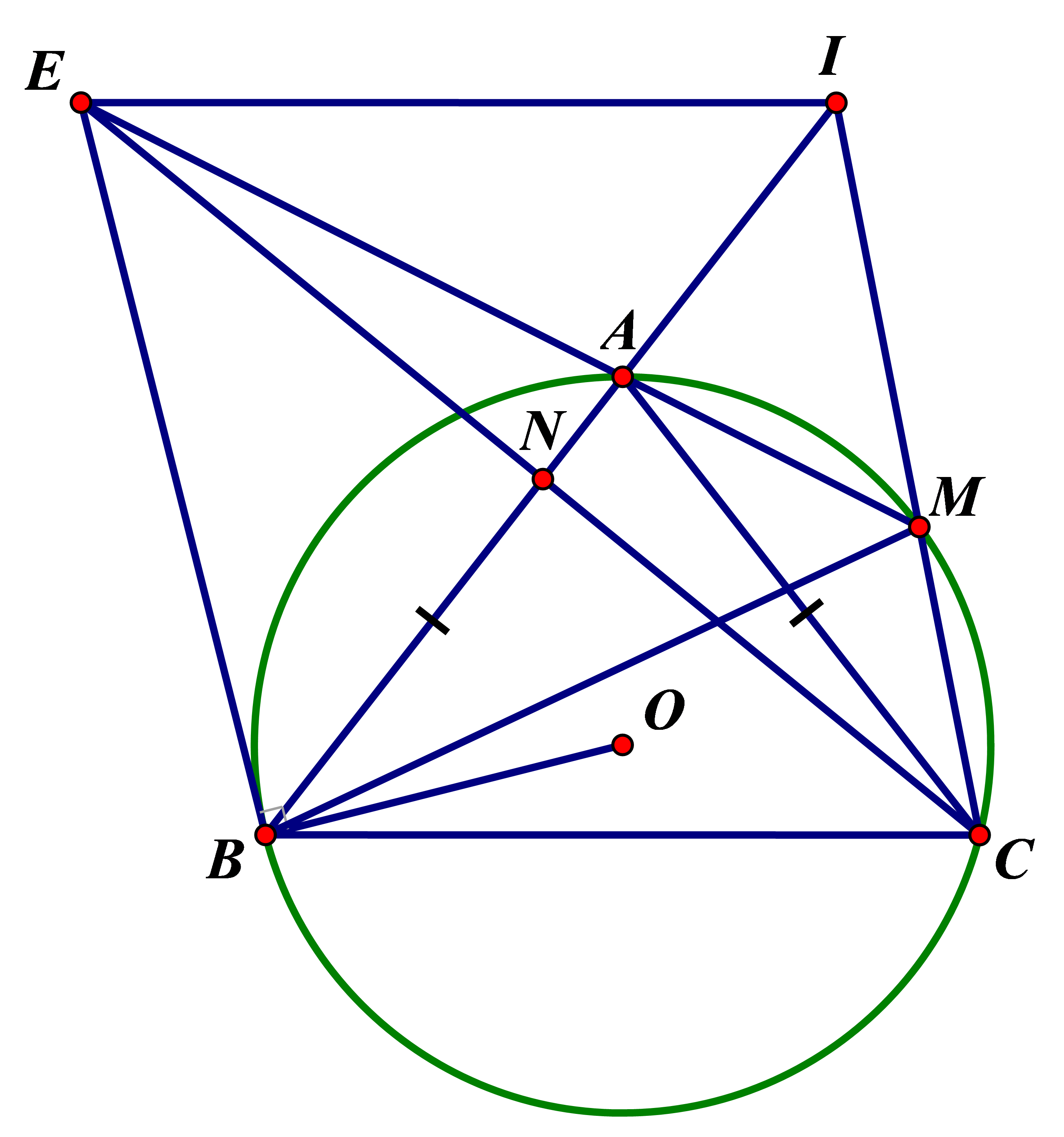
a. Xét tứ giác AMCB có 4 điểm A, M, C, B thuộc đường tròn (O)

Suy ra tứ giác AMCB nội tiếp.

Ta có

$\widehat{AMB}=\widehat{ACB}$ (tứ giác AMCB nội tiếp)

$\widehat{ABC}=\widehat{ACB}$ (tam giác ABC cân tại A)

Suy ra $\widehat{AMB}=\widehat{ABC}$ (điều phải chứng minh)

b. Xét ∆ AIC và ∆ MIB có:

$\widehat{\text{BIC}}$ là góc chung

$\widehat{\text{IBM}}\text{=}\widehat{\text{ICA}}$(hai góc nội tiếp cùng chắn cung AM)

Suy ra ∆ AIC  ∆ MIB (g.g)

Từ đó suy ra $\frac{\text{IA}}{\text{IM}}\text{=}\frac{\text{IC}}{\text{IB}}\iff$ IA.IB = IM.IC (đpcm)

c. Ta có

$\widehat{EBI}=\widehat{ACB}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB)

$\widehat{EMI}=\widehat{ABC}$ (tứ giác AMCB nội tiếp)

$\widehat{ABC}=\widehat{ACB}$ (tam giác ABC cân tại A)

Từ ba điều trên suy ra $\widehat{EBI}=\widehat{EMI}$ suy ra tứ giác BEIM nội tiếp.

d. Ta có $\widehat{EIB}=\widehat{EMB}$(tứ giác EIMB nội tiếp)

$\widehat{EMB}=\widehat{AMB}=\widehat{ABC}=\widehat{IBC}$(chứng minh trên)

Suy ra $\widehat{EIB}=\widehat{IBC}$ suy ra IE // BC (hai góc so le trong bằng nhau).

Áp dụng hệ quả của định lý Ta − let ta có:

$\frac{NE}{NC}=\frac{NI}{NB}=\frac{EI}{BC}$$\Rightarrow \frac{NE.NI}{NC.NB}=\frac{E{I}^2}{B{C}^2}$ (1)

Ta có $\widehat{EIB}=\widehat{EMB}$(tứ giác EIMB nội tiếp).

$\widehat{EMB}=\widehat{EBI}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB).

Suy ra $\widehat{EBI}=\widehat{EBI}$ suy ra tam giác EBI cân tại E dẫn đến EB = EI (2)

Từ (1) và (2) suy ra ${\left(\frac{BE}{BC}\right)}^2=\frac{NE.NI}{NB.NC}$ (điều phải chứng minh).