Cho nửa đường tròn (O) đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn. Gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA, D là một điểm tùy ý trên cung CB (D khác...

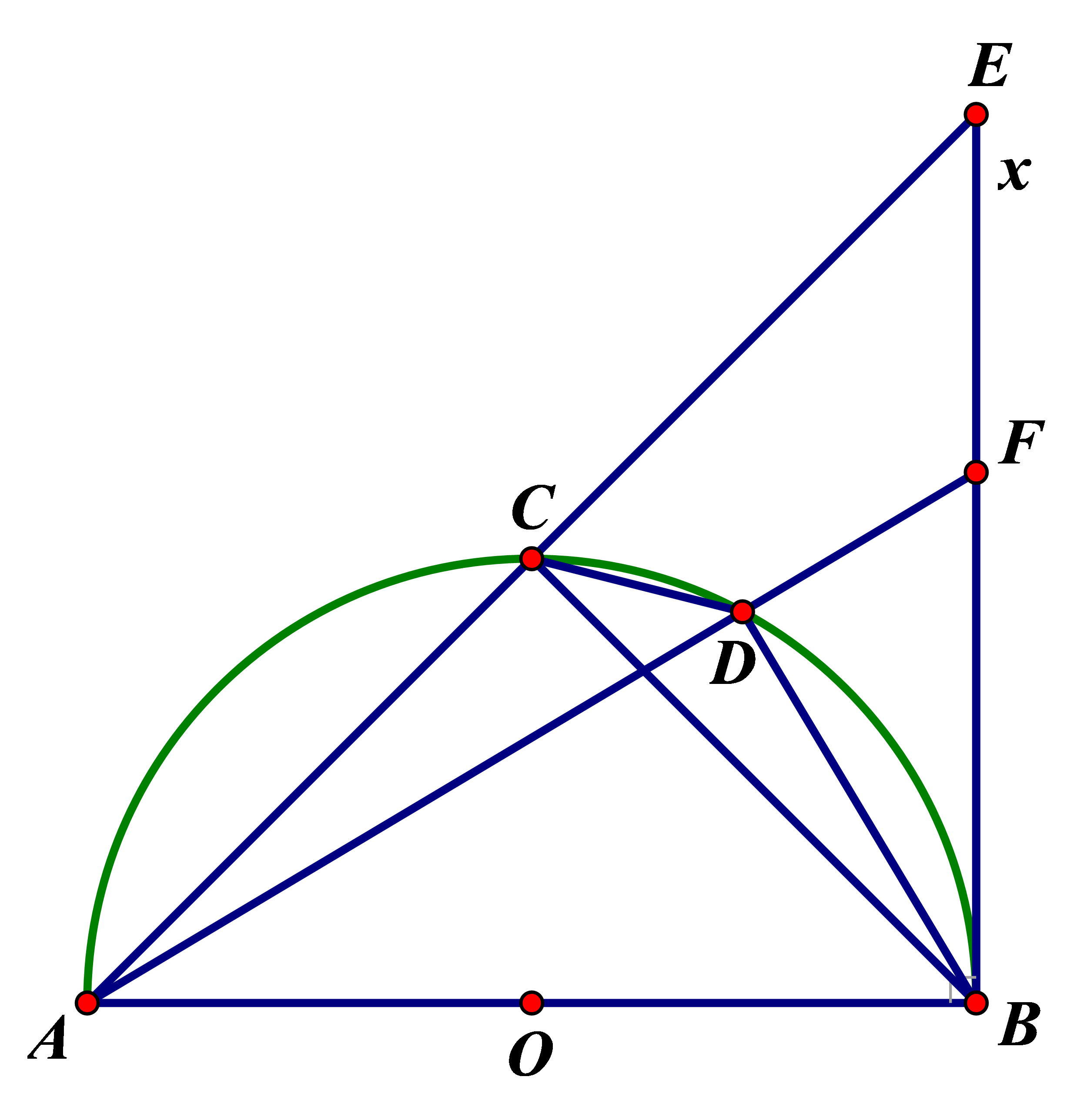
a. Ta có $\widehat{CAB}=\widehat{CBA}$(hai góc nội tiếp chắn hai cung bằng nhau)

Ta lại có $\widehat{ACB}$= 90° (góc nội tiếp chắn nửa đường tròn)

Suy ra tam giác CAB là tam giác vuông cân và $\widehat{CAB}$= 45°

Xét tam giác ABE vuông tại B (Bx là tiếp tuyến của (O)) có $\widehat{EAB}$= 45°

Dẫn đến $\widehat{AEB}$ = 180° − $\widehat{ABE}-\widehat{EAB}$= 180 – 90 – 45 = 45° = $\widehat{EAB}$

Suy ra tam giác ABE là tam giác vuông cân.

b. Xét ∆ FDB và ∆ FBA có:

$\widehat{AFB}$là góc chung

$\widehat{FBA}$= $\widehat{ADB}$ = 90° ($\widehat{ADB}$ là góc nội tiếp chắn nữa đường tròn và Bx là tiếp tuyến của (O))

Suy ra ∆ FDB  ∆ FBA (g.g)

Từ đó suy ra $\frac{FB}{FA}\text{=}\frac{\text{FD}}{\text{FB}}\iff$ FB² = FD.FA (đpcm)

c. Từ câu b ta suy ra được: Trong một tam giác vuông thì bình phương cạnh góc vuông bằng tích hình chiếu của nó trên cạnh huyền nhân với cạnh huyền.

Xét tam giác ABF vuông tại B đường cao BD ta có: AB² = AD.AF

 ABE vuông tại B đường cao BC ta có: AB² = AC.AE

Suy ra AD.AF = AC.AE $\iff \frac{AD}{AE}=\frac{AC}{AF}$

Xét ∆ ACD và ∆ AFE có:

$\widehat{EAF}$là góc chung

$\frac{AD}{AE}=\frac{AC}{AF}$ (chứng minh trên)

Suy ra ∆ ACD  ∆ AFE (c.g.c)

Suy ra $\widehat{CDA}=\widehat{CEF}$ suy ra tứ giác CDFE là tứ giác nội tiếp.