Cho hàm số y = mx^2 có đồ thị là parabol (P) và đường thẳng (d): y = 3x + 4. a) Tìm giá trị của m, biết (P) đi qua điểm M(1; 1). Vẽ (P) trên mặt phẳng tọa độ Oxy với giá trị của m...
Câu hỏi :
Cho hàm số y = mx2 có đồ thị là parabol (P) và đường thẳng (d): y = 3x + 4.
a) Tìm giá trị của m, biết (P) đi qua điểm M(1; 1). Vẽ (P) trên mặt phẳng tọa độ Oxy với giá trị của m vừa tìm được.
b) Với giá trị nào của m tìm được ở câu a, tìm tọa độ các giao điểm của (d) và (P).
Cho hàm số y = mx2 có đồ thị là parabol (P) và đường thẳng (d): y = 3x + 4.
a) Tìm giá trị của m, biết (P) đi qua điểm M(1; 1). Vẽ (P) trên mặt phẳng tọa độ Oxy với giá trị của m vừa tìm được.
b) Với giá trị nào của m tìm được ở câu a, tìm tọa độ các giao điểm của (d) và (P).
* Đáp án
* Hướng dẫn giải
a) Do (P) đi qua M nên thay giá trị của M(1; 1) vào hàm số y = mx2 ta được
1 = m.12 m = 1
Vậy (P): y = x2
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Do đó (P) đi qua các điểm (−2; 4); (−1; 1); (0; 0); (1; 1); (2; 4).
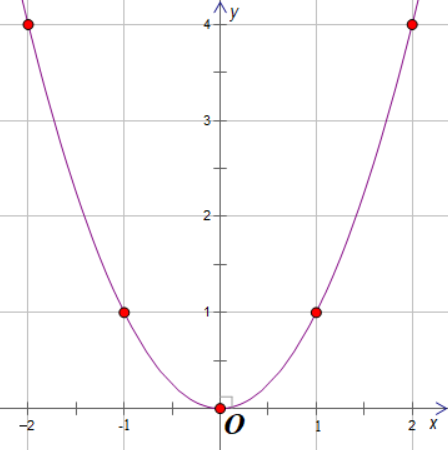
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 3x + 4
Û x2 − 3x – 4 = 0
Û x2 + x – 4x – 4 = 0
Û x(x + 1) – 4(x + 1) = 0
Û (x – 4)(x + 1) = 0
Û
• Với x = 4 thì y = 3x + 4 = 3.4 + 4 = 16.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(4; 16).
• Với x = –1 thì y = 3x + 4 = 3.(–1) + 4 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(−1; 1).
Vậy tọa độ các giao điểm của (d) và (P) là A(4; 16) và B(−1; 1).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
