Cho ∆ABC nhọn nội tiếp đường tròn (O) với AB < AC. Các đườ
Câu hỏi :
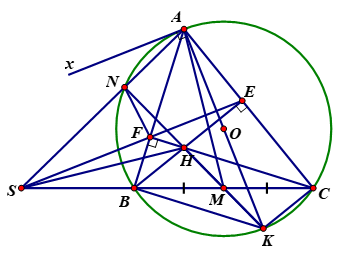
Cho ∆ABC nhọn nội tiếp đường tròn (O) với AB < AC. Các đường cao BE và CF của ∆ABC cắt nhau tại H.
1) Chứng minh tứ giác BCEF nội tiếp.
2) Chứng minh OA ⊥ EF.
3) Gọi M là trung điểm của BC, S là giao điểm của đường thẳng EF và BC. Kẻ đường kính AK của đường tròn (O). Chứng minh H, M, K thẳng hàng và chứng minh SH ⊥ AM.
Cho ∆ABC nhọn nội tiếp đường tròn (O) với AB < AC. Các đường cao BE và CF của ∆ABC cắt nhau tại H.
1) Chứng minh tứ giác BCEF nội tiếp.
2) Chứng minh OA ⊥ EF.
3) Gọi M là trung điểm của BC, S là giao điểm của đường thẳng EF và BC. Kẻ đường kính AK của đường tròn (O). Chứng minh H, M, K thẳng hàng và chứng minh SH ⊥ AM.
* Đáp án
* Hướng dẫn giải
) Ta có (CF ⊥ AB)
(BE ⊥ AC)
Xét tứ giác BFEC có
Suy ra tứ giác BFEC nội tiếp.
2) Từ A kẻ tiếp tuyến Ax của (O)
Ta có (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB)
Mà (tứ giác FECB nội tiếp)
Suy ra Ax // FE (hai góc so le trong)
Mà Ax ⊥ AO (Ax là tiếp tuyến của (O))
Suy ra FE ⊥ OA (điều phải chứng minh)
3) Ta có: (góc nội tiếp chắn nửa đường tròn)
(góc nội tiếp chắn nửa đường tròn)
Xét tứ giác BHCK có:
BH // CK (cúng vuông góc AC)
CH // BK (cùng vuông góc AB)
Suy ra tứ giác BHCK là hình bình hành
Tứ giác BHCK là hình bình hành có M là trung điểm BC
Suy ra M cũng là trung điểm HK suy ra M, H, K thẳng hàng
SA cắt đường tròn (O) tại N
Xét tứ giác nội tiếp BFEC có FE cắt BC tại S
Xét ∆SFB và ∆SCE có:
là góc chung
(tứ giác BFEC nội tiếp)
Suy ra ∆SFB ![]() ∆SCE (g.g)
∆SCE (g.g)
Suy ra
Tương tự tứ giác BNAC nội tiếp (O) có AN cắt CB tại S.
Suy ra SN.SA = SB.SC
Từ 2 điều trên suy ra SN.SA = SF.SE
Xét ∆SNF và ∆SEA có:
là góc chung
(chứng minh trên)
Do đó ∆SNF ![]() ∆SEA (c.g.c)
∆SEA (c.g.c)
Suy ra .
Suy ra tứ giác ANFE nội tiếp (1)
Ta có (CF ⊥ AB)
(BE ⊥ AC)
Xét tứ giác AFHE có
Suy ra tứ giác AFHE nội tiếp. (2)
Từ (1) và (2) suy ra A, N, F, H, E nội tiếp cùng một đường tròn.
Có (BE ⊥ AC) AH là đường kính .
Suy ra (góc nội tiếp chắn nửa đường tròn)
.
Ta có (góc nội tiếp chắn nửa đường tròn)
.
Mà NH ⊥ SA (cmt).
Suy ra K, H, N thẳng hàng hay 4 điểm K, M, H, N thẳng hàng.
Suy ra MH ⊥ SA.
Xét tam giác ABC có H là giao điểm của 2 đường cao CF và BE.
Suy ra AH là dường cao thứ ba suy ra AH ⊥ BC hay AH ⊥ SM.
Xét tam giác ASM có:
MH ^ SA (cmt);
AH ^ SM (cmt).
Suy ra H là trực tâm của tam giác ASM.
Vậy SH ⊥ AM (điều phải chứng minh).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
