Trên mặt phẳng tọa độ Oxy cho đường thẳng (d): y = x + 4 và
Câu hỏi :
Trên mặt phẳng tọa độ Oxy cho đường thẳng (d): y = x + 4 và (P):
a. Nêu đặc điểm của đồ thị hàm số .
b. Vẽ đồ thị (P): .
c. Tìm tọa độ các giao điểm A và B của (d) và (P).
d. Tìm tọa độ điểm M trên tia Ox có hoành độ lớn hơn 4 sao cho diện tích ∆MAB bằng 30 (đvdt) với A, B là giao điểm của (d) và (P).
Trên mặt phẳng tọa độ Oxy cho đường thẳng (d): y = x + 4 và (P):
a. Nêu đặc điểm của đồ thị hàm số .
b. Vẽ đồ thị (P): .
c. Tìm tọa độ các giao điểm A và B của (d) và (P).
d. Tìm tọa độ điểm M trên tia Ox có hoành độ lớn hơn 4 sao cho diện tích ∆MAB bằng 30 (đvdt) với A, B là giao điểm của (d) và (P).
* Đáp án
* Hướng dẫn giải
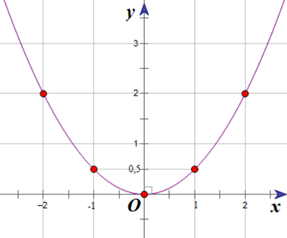
a. Đồ thị hàm số là đường cong đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. Đường cong này gọi là parabol với đỉnh O với O là điểm thấp nhất của đồ thị hàm số.
b. Vẽ (P)
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
|
2 |
0,5 |
0 |
0,5 |
2 |
Parabol (P) đi qua các điểm (0; 0); (−2; 2); (−1; 0,5); (1; 0,5); (2; 2).
Ta có đồ thị hàm số (P):
.
c. Phương trình hoành độ giao điểm của (P) và (d) là:
Û x2 – 2x – 8 = 0
Û x2 – 4x + 2x – 8 = 0
Û x(x – 4) + 2(x – 4) = 0
Û (x + 2)(x – 4) = 0
• Với x = −2 thì y = x + 4 = –2 + 4 = 2.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(−2; 2).
• Với x = 4 thì y = x + 4 = 4 + 4 = 8.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(4; 4).
Vậy hai đồ thị hàm số trên có 2 giao điểm là A(−2; 2) và B(4; 4).
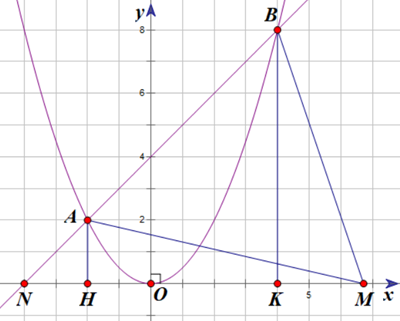
Gọi N là giao điểm của (d) và Ox khi đó tọa độ của N là = (-4; 0)
Kẻ AH và BK vuông góc với Ox (H, K ∈ Ox).
Với xM > 4 ta có:
SMAB = SBNM − SANM =
Theo đề bài ta có SMAB = 3(xM + 4) = 30
Û xM + 4 = 10
Û xM = 6
Vậy M(0;6)
Û xM + 4 = 10
Û xM = 6
Vậy M(0; 6) thì SMAB = 30 (đvdt)
(0; 6) thì SMAB = 30 (đvdt)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
