): Cho nửa đường tròn (O; R) đường kình AB. Điểm C di động

Câu hỏi :

Cho nửa đường tròn (O; R) đường kình AB. Điểm C di động trên nửa đường tròn (C khác A và B), gọi M là điểm chính giữa cung AC. BM cắt AC tại H và cắt tia tiếp tuyến Ax của nửa đường tròn (O) tại K, AM cắt BC tại D.

a. Chứng minh tứ giác DMHC nội tiếp.

b. Chứng minh ∆ABM đồng dạng với ∆HBC suy ra BH.BM = BA.BC

c. Tứ giác AKDH là hình gì? Tại sao?

d. Đường tròn ngoại tiếp ∆BHD cắt đường tròn (B; BA) tại N. Chứng minh A, C, N thẳng hàng.

* Đáp án

* Hướng dẫn giải

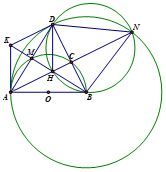
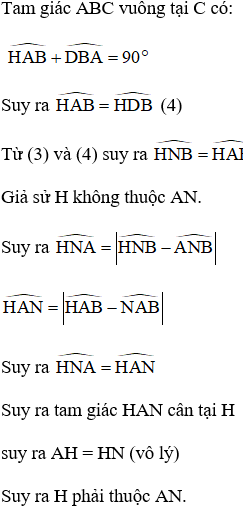
Mà C thuộc AH suy ra ba điểm

 A, C, N thẳng hàng