Cho tam giác EFK vuông tại F, có FE = 10, 5 cm; FK = 14 cm a) Giải tam giác EFK

Câu hỏi :

Cho tam giác EFK vuông tại F, có FE = 10, 5 cm; FK = 14 cm

a) Giải tam giác EFK

b) Gọi FH là đường cao, FA là đường trung tuyến của $\Delta EFK$ . Tính FH, FA

c) Tính góc tạo bởi FH với FA

d) Bỏ qua các số liệu đã cho ở trên. Kẻ $HB\perp FE$ tại B, $HC\perp FK$ tại C

Chứng minh ${\cot }^{3}E=\frac{BE}{CK}$ 

* Đáp án

* Hướng dẫn giải

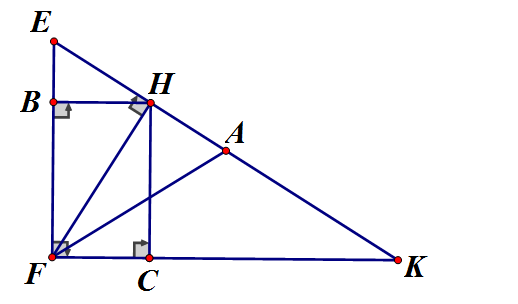
a) Áp dụng định lý Pytago và $\Delta EFK$ $\Rightarrow EK=\sqrt{E{F}^2+F{K}^2}$

$=\sqrt{10,5^2+{14}^2}=17,5\left(cm\right)$
$\begin{array}{l}\sin E=\frac{FK}{EK}=\frac{14}{17,5}=\frac{4}{5}\Rightarrow \widehat{E}\approx {53}^0\\ \Rightarrow \widehat{K}\approx {90}^0-\widehat{E}={90}^0-{53}^0={37}^0\end{array}$
Vậy $\widehat{E}={53}^0,\widehat{K}={37}^0,EK=17,5cm.$

b)

a)     Áp dụng hệ thức lượng vào tam giác vuông FEK vuông tại F,  FK đường cao

     $\begin{array}{l}\Rightarrow \frac{1}{F{H}^2}=\frac{1}{F{E}^2}+\frac{1}{F{K}^2}=\frac{1}{10,5^2}+\frac{1}{{14}^2}\\ \Rightarrow \frac{1}{F{H}^2}=\frac{25}{1764}\Rightarrow FH=8,4\left(cm\right)\end{array}$

    c)

a)     Ta có $\Delta FEK$ vuông tại F, F, FA là đường trung tuyến

$\Rightarrow FA=\frac{1}{2}EK=\frac{1}{2}.17,5=8,75\left(cm\right)$
$\cos \widehat{HFA}=\frac{FH}{FA}=\frac{8,4}{8,75}=\frac{24}{25}\Rightarrow \widehat{HFA}\approx {16}^0$

d) Áp dụng tính chất các góc phụ nhau trong tam giác vuông ta có:

$\widehat{E}=\widehat{BHF}=\widehat{HFK}=\widehat{CHK}$

Ta có : BHCF là hình chữ nhật vì có 3 góc vuông $\Rightarrow BF=CH.$ Ta có:

$\begin{array}{l}\cot \widehat{E}=\frac{BE}{BH};\cot \widehat{BHF}=\frac{BH}{BF};\cot \widehat{CHK}=\frac{CH}{CK}=\frac{BF}{CK}\\ \Rightarrow {\cot }^{3}E=\frac{BE}{BH}.\frac{BH}{BF}.\frac{BF}{CK}=\frac{BE}{CK}\left(dfcm\right)\end{array}$