Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại S. Kẻ tiếp tuyến chung ngoài

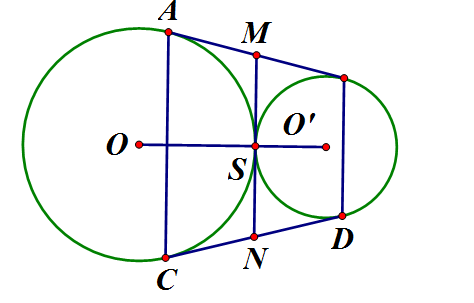
Vẽ tiếp tuyến chung tại S lần lượt cắt AB, CD ở M, N. Theo tính chất tiếp tuyến ta có:

$\left\{\begin{array}{l}AM=SM=BM\\ CN=SN=DN\end{array}\right.$ do đó: $AB+CD=2MN\left(1\right)$

Mặt khác OO' là trục đối xứng của hình nên C đối xứng với A qua OO', D đối xứng với B qua OO' nên $AC\perp OO\text{'},BD\perp OO\text{'}$ do đó $AC//BD\Rightarrow ABCD$ là hình thang.

M, N lần lượt là trung điểm của AB, CD nên MN là đường trung bình hình thang ABCD.

$\Rightarrow AC+BD=2MN\left(2\right)$

Từ (1) và (2) suy ra $AB+CD=AC+BD.$