Cho tam giác ABC vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường kính BC

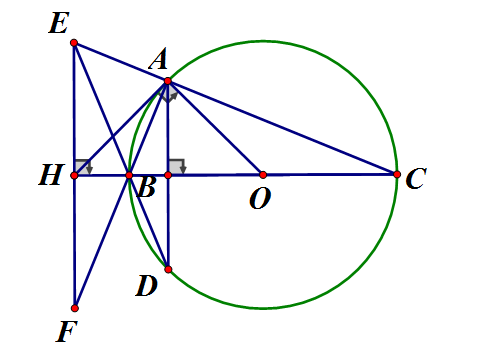
a) Vì AD // EF (cùng vuông góc BC)$\Rightarrow \widehat{ADE}=\widehat{DEF}$ (so le trong ) (1)

Ta lại có $\Delta ABD$ có BO vừa là đường cao vừa là đường trung tuyến (tính chất tiếp tuyến – dây cung) nên $\Delta ABD$ cân tại $B\Rightarrow \widehat{ADE}=\widehat{BAD}\left(2\right)$ mà $\widehat{BAD}=\widehat{BFE}$ (so le trong) (3)

Từ (1), (2), (3)$\Rightarrow \widehat{DEF}=\widehat{BFE}\Rightarrow \Delta EBF$ cân tại B

b) $\Delta EBF$ cân tại B $\Rightarrow BH$ đường cao cũng là trung tuyến $\Rightarrow B$ là trung điểm EF $\Rightarrow \Delta E\text{}AF$ vuông tại A, AH đường trung tuyến

$\Rightarrow AH=EH=FH=\frac{EF}{2}\Rightarrow \Delta HAF$ cân tại H

c) Vì $\Delta HAF$ cân tại H$\Rightarrow \widehat{F}=\widehat{HAB}\left(4\right)$ mà $\widehat{F}=\widehat{C}$ (cùng phụ góc E) (5)

$\widehat{C}=\widehat{OAC}(\Delta AOC$ cân ) (6)

Từ (4), (5), (6) $\Rightarrow \widehat{HAB}=\widehat{AOC}$

$\Rightarrow \widehat{HAB}+\widehat{BAO}=\widehat{BAO}+\widehat{OAC}\Rightarrow \widehat{HAO}=\widehat{BAC}={90}^0$

$\Rightarrow AH\perp AO$ và $A\in \left(O\right)\Rightarrow AH$ là tiếp tuyến của (O).