Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O

Câu hỏi :

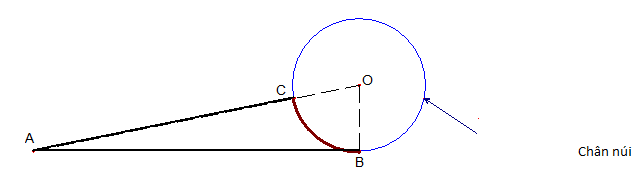
Có một vụ tai nạn ở vị trí B tại chân của một ngọn núi (chân núi có dạng đường tròn tâm O, bán kính 3 km) và một trạm cứu hộ ở vị trí A (tham khảo hình vẽ). Do chưa biết đường đi nào để đến vị trí tai nạn nhanh hơn nên đội cứu hộ quyết định điều hai xe cứu thương cùng xuất phát ở trạm đến vị trí tai nạn theo hai cách sau:

Xe thứ nhât : đi theo đường thẳng từ A đến B, do đường xấu nên vận tốc trung bình của xe là 40 km/h.

Xe thứ hai: đi theo đường thẳng từ A đến C với vận tốc trung bình 60 km/h, rồi đi từ C đến B theo đường cung nhỏ CB ở chân núi với vận tốc trung bình 30 km/h ( 3 điểm A, O, C thẳng hàng và C ở chân núi). Biết đoạn đường AC dài 27 km và $\widehat{ABO}={90}^0$ .

a) Tính độ dài quãng đường xe thứ nhất đi từ A đến B.

b) Nếu hai xe cứu thương xuất phát cùng một lúc tại A thì xe nào thì xe nào đến vị trí tai nạn trước ?