Cho đường tròn (O) đường kính AB = 2R.

* Hướng dẫn giải

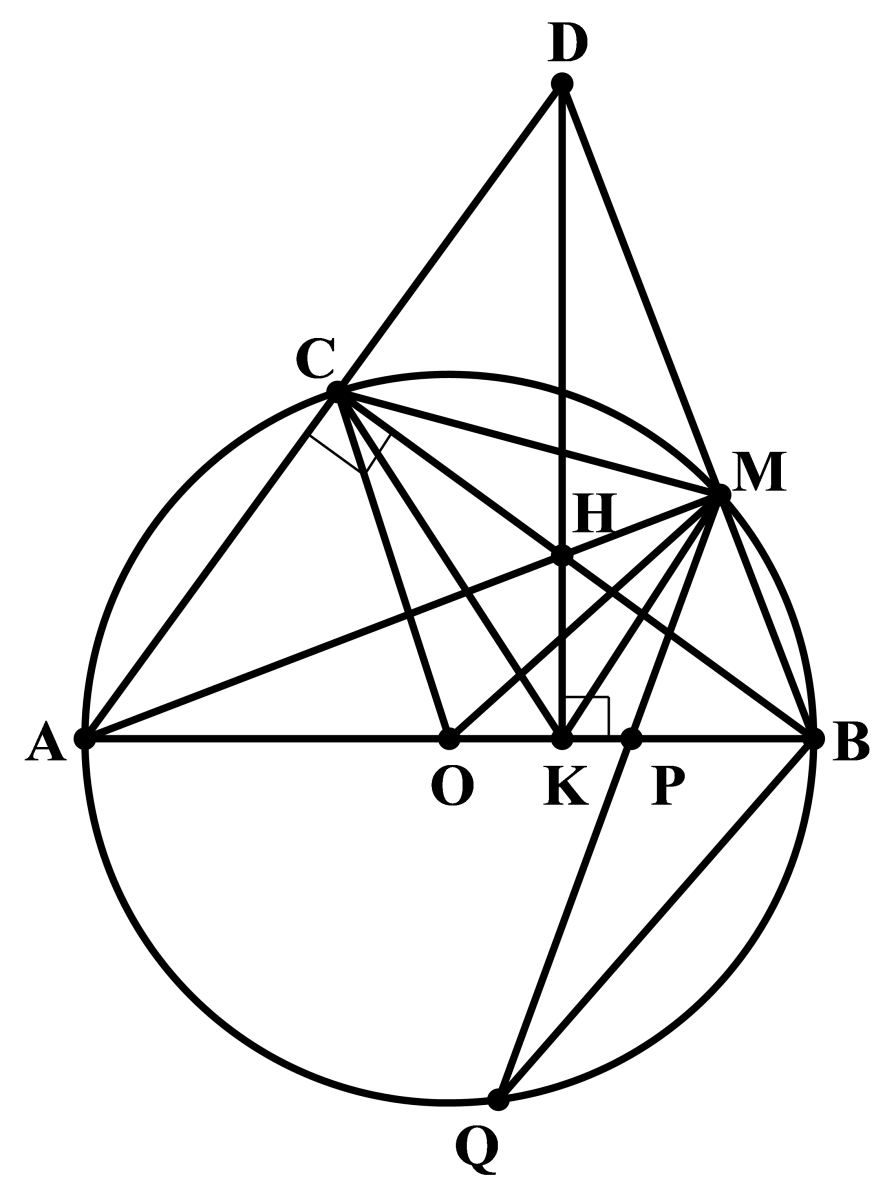
1) Ta có \(\widehat {ACB} = \widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

Xét tứ giác BKHM có \(\widehat {ACB} + \widehat {AMB} = {180^0},\) suy ra CDMH nội tiếp đường tròn.

Vậy bốn điểm C, D, M, H cùng thuộc một đường tròn.

2) Tam giác ABD nhận H là trực tâm vì có hai đường cao BC và AM cắt nhau tại H,

Suy ra DH là đường cao trong tam giác ABD, do đó: \(DK \bot AB\) (1)

3) Ta có tứ giác AKHC nội tiếp, suy ra \(\widehat {CAH} = \widehat {CKH}\).

Và tứ giác BKHM nội tiếp, suy ra \(\widehat {HBM} = \widehat {MKH}\).

Mà \(\widehat {CAH} = \widehat {HBM}\) (cùng chắn cung CN của (O)), do đó: \(\widehat {CKM} = 2\widehat {CAH}\)

Mặt khác, xét (O) có \(\widehat {COM} = 2\widehat {CAH}\) (góc ở tâm và góc nội tiếp).

Do đó, \(\widehat {CKM} = \widehat {COM}\).

Suy ra tứ giác COKM nội tiếp, suy ra đường tròn ngoại tiếp tam giác CKM cũng là đường tròn ngoại tiếp tứ giác COKM . 

4) Gọi Q là giao điểm của MP với (O).

Ta có \(\Delta QAB\) là tam giác vuông cân tại Q, suy ra \(AQ = \frac{{AB}}{{\sqrt 2 }} \Rightarrow \frac{{AB}}{{AQ}} = \sqrt 2 .\)

Ta có \(\Delta MPA{\rm{ }} \sim {\rm{ }}\Delta BPQ\) (g – g) \( \Rightarrow \frac{{MP}}{{MA}} = \frac{{BP}}{{BQ}}.\)

Tương tự \(\Delta MPB{\rm{ }} \sim {\rm{ }}\Delta APQ\) (g – g) \( \Rightarrow \frac{{MP}}{{MB}} = \frac{{AP}}{{AQ}}.\)

Do đó \(\frac{{MP}}{{MA}} + \frac{{MP}}{{MB}} = \frac{{BP}}{{BQ}} + \frac{{AP}}{{AQ}} = \frac{{AB}}{{AQ}} = \sqrt 2 \).

Mặt khác, ta có \(\frac{{MP}}{{MA + MB}} \le MP.\frac{1}{4}\left( {\frac{1}{{MA}} + \frac{1}{{MB}}} \right) = \frac{{\sqrt 2 }}{4}.\)

Vậy max \(\frac{{MP}}{{MA + MB}} = \frac{{\sqrt 2 }}{4}\) khi MA = MB hay M là điểm chính giữa cung AB.