Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Toán 9 phần Hình học Tập 2 !!
Cho hình bình hành ABCD. Đường tròn đi qua ba...
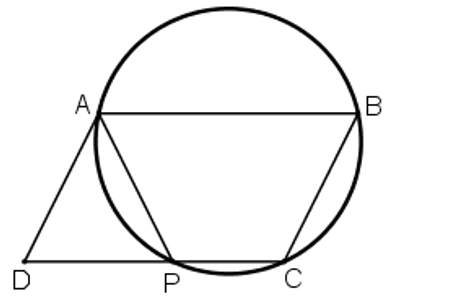
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C
Câu hỏi :
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.
* Đáp án
* Hướng dẫn giải
+ Do ABCD là hình bình hành nên AB//CD
(hai góc trong cùng phía) (1)
+ ABCP là tứ giác nội tiếp
Từ (1) và (2) suy ra:
+ Tứ giác ABCP có: AB//CP (vì AB//CD)
=> Tứ giác ABCP là hình thang.
Lại có: nên ABCP là hình thang cân.
=> AP=BC (3)
Mà ABCD là hình bình hành => AD = BC (4)
Từ (3) và (4) suy ra AP=AD (đpcm).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Toán 9 phần Hình học Tập 2 !!
Số câu hỏi: 271
Copyright © 2021 HOCTAP247