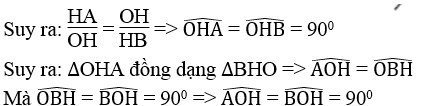Cho hai đường thẳng: y = ax + b (d) y = a’x + b’ (d’) Chứng minh rằng: Trên cùng một mặt

* Hướng dẫn giải

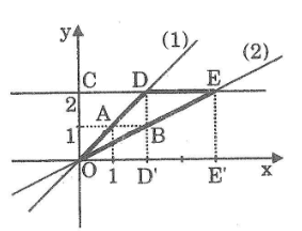
Qua gốc tọa độ, kẻ đường thẳng y = ax // (d) và y = a’x // (d’)

*Chứng minh (d) vuông góc với (d’) thì a.a’ = -1

Không mất tính tổng quát, giả sử a > 0

Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.

Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù (vì các góc tạo bởi đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau 900).

Suy ra: a’ < 0

Mà đường thẳng y = ax đi qua A(1; a), đường thẳng y = a’x đi qua B(1; a’) nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.

Vì (d) ⊥ (d’) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau. Suy ra: góc(AOB) = $90°$

Tam giác vuông AOB có OH ⊥ AB. Theo hệ thức lượng trong tam giác vuông, ta có: OH2 = HA.HB

Hay: a.|a’| = 1 ⇔ a.(-a’) = 1 ⇔ a.a’ = -1

Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1

*Chứng minh a.a’ = -1 thì (d) vuông góc với (d’)

Ta có: a.a’ = -1 ⇔ a.|a’| = 1 hay HA.HB = $O{H}^2$

Suy ra OA ⊥ OB hay hai đường thẳng y = ax và y = a’x vuông góc với nhau hay (d) ⊥ (d’)