Cho tam giác ABC có góc A = 60 độ. Chứng minh rằng: BC^2 = AB^2 + AC^2

* Hướng dẫn giải

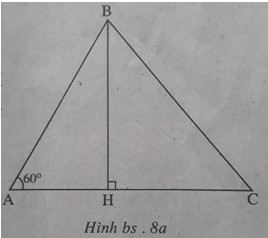
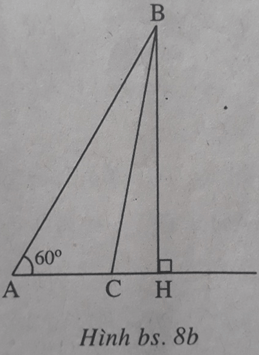
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để $\angle$(BAC) = $60°$ là góc nhọn), do đó $H{C}^2={\left(AC-AH\right)}^2$(xem h.bs.8a, 8b)

Công thức Py-ta-go cho ta

$$\begin{gathered} B{C}^2=B{H}^2+H{C}^2 \\ =B{H}^2+{\left(AC-AH\right)}^2 \\ =B{H}^2+A{C}^2+A{H}^2-2AC.AH \\ =A{B}^2+A{C}^2-2AC.AH \end{gathered}$$

Do $\angle$(BAC) = $60°$ nên AH = AB.cos$60°$ = AB/2, suy ra $B{C}^2=A{B}^2+A{C}^2-AB.AC$