Cho tứ giác ABCD có anpha là góc nhọn tạo bởi hai đường chéo chứng

* Hướng dẫn giải

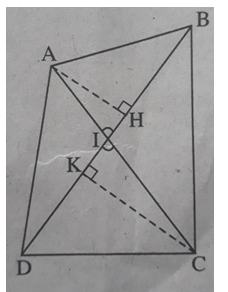
Giả sử hai đường chéo AC, BD cắt nhau tại I, $\angle$(AIB) = $\alpha$ là góc nhọn (xem h.bs.9)

Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.

Ta có: AH = AI.sin$\alpha$, CK = CI.sin$\alpha$

Diện tích tam giác ABD là $S_{ABD}$ = 1/2 BD.AH.

Diện tích tam giác CBD là $S_{CBD}$ = 1/2 BD.CK.

Từ đó diện tích S của tứ giác ABCD là:

S = $S_{ABD}+S_{CBD}$ = 1/2BD.(AH + CK)

= 1/2 BD.(AI + CI)sin$\alpha$ = 1/2BD.AC.sin$\alpha$