Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Sách Bài Tập Toán 9 Tập 1 !!
Cho hình bên, trong đó có hai dây CD, EF...
Cho hình bên, trong đó có hai dây CD, EF bằng nhau và vuông góc
Câu hỏi :
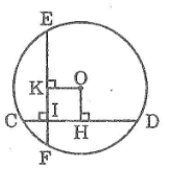
Cho hình bên, trong đó có hai dây CD, EF bằng nhau và vuông góc với nhau tại I, IC = 2cm, ID = 14cm. Tính khoảng cách từ O đến mỗi dây
* Đáp án
* Hướng dẫn giải
Kẻ OH ⊥ CD, OK ⊥ EF
Vì tứ giác OKIH có ba góc vuông nên nó là hình chữ nhật.
Ta có: CD = EF (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Suy ra tứ giác OKIH là hình vuông.
Ta có:
CD = CI + ID = 2 + 14 = 16(cm)
HC = HD = CD/2 = 8 (cm) (đường kính dây cung)
IH = HC - CI = 8 - 2 = 6 (cm)
Suy ra: OH = OK = 6 (cm) (OKIH là hình vuông)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 1 !!
Số câu hỏi: 814
Copyright © 2021 HOCTAP247