Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Sách Bài Tập Toán 9 Tập 1 !!
Cho đường tròn (O), hai dây AB, CD cắt nhau...
Cho đường tròn (O), hai dây AB, CD cắt nhau tại điểm M nằm bên
Câu hỏi :
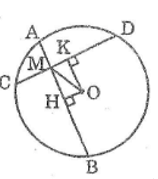
Cho đường tròn (O), hai dây AB, CD cắt nhau tại điểm M nằm bên trong đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Cho biết AB > CD, chứng minh rằng MH > MK.
* Đáp án
* Hướng dẫn giải
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
Suy ra : (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
Suy ra: (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: hay HM > KM
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 1 !!
Số câu hỏi: 814
Copyright © 2021 HOCTAP247