Cho đường tròn (O) và đường thẳng d không giao nhau. Dựng tiếp tuyến của

* Hướng dẫn giải

* Phân tích

Giả sử tiếp tuyến của đường tròn dựng được thỏa mãn điều kiện bài toán

- $d_1$ là tiếp tuyến của đường tròn tại A nên $d_1$ ⊥ OA

- Vì $d_1$ // d nên d ⊥ OA

Vậy A là giao điểm của đường thẳng kẻ từ O vuông góc với d

* Cách dựng

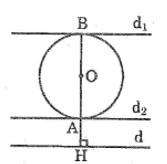
- Dựng OH vuông góc với d cắt đường tròn (O) tại A và B

- Dựng đường thẳng $d_1$ đi qua A và vuông góc với OA

- Dựng đường thẳng $d_2$ đi qua B và vuông góc với OB

Khi đó $d_1$ và $d_2$ là hai tiếp tuyến cần dựng.

* Chứng minh

Ta có: A và B thuộc (O)

$d_1$ // d mà d ⊥ OH nên $d_1$ ⊥ OH hay $d_1$ ⊥ OA tại A

Suy ra $d_1$ là tiếp tuyến của đường tròn (O)

$d_2$ // d mà d ⊥ OH nên $d_2$ ⊥ OH hay $d_2$ ⊥ OB tại B

Suy ra $d_2$ là tiếp tuyến của đường tròn (O)

* Biện luận

Đường thẳng OH luôn cắt đường tròn (O) nên giao điểm A và B luôn dựng được.