Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Sách Bài Tập Toán 9 Tập 1 !!
Cho nửa đường tròn tâm O đường kính AB. Gọi...
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông
Câu hỏi :
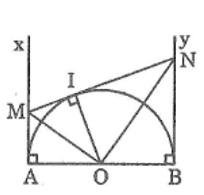
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Chứng minh rằng AM.BN = (R là bán kính của nửa đường tròn)
* Đáp án
* Hướng dẫn giải
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
= MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = =
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 1 !!
Số câu hỏi: 814
Copyright © 2021 HOCTAP247