Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Sách Bài Tập Toán 9 Tập 1 !!
Cho nửa đường tròn tâm O có đường kính AB....
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax
Câu hỏi :
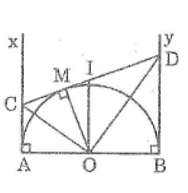
, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất
* Đáp án
* Hướng dẫn giải
Theo tính chất hai tiếp tuyến cắt nhau ta có:
CA = CM
DB = DM
Suy ra: AC + BD = CM + DM = CD
Chu vi hình thang ABDC bằng: AB + BD + DC + CA = AB + 2CD
Vì đường kính AB của (O) không thay đổi nên chu vi hình thang nhỏ nhất khi CD nhỏ nhất
Ta có: CD AB nên CD nhỏ nhât khi và chỉ khi CD = AB
Khi đó CD // AB ⇔ OM ⊥ AB
Vậy khi M là giao điểm của đường thẳng vuông góc với AB tại O với nửa đường tròn (O) thì hình thang ABDC có chu vi nhỏ nhất.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 1 !!
Số câu hỏi: 814
Copyright © 2021 HOCTAP247