Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Sách Bài Tập Toán 9 Tập 1 !!
Cho hai đường tròn (O) và (O’) cắt nhau tại...
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung
Câu hỏi :
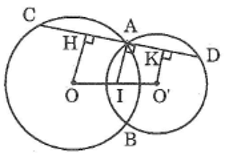
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD
* Đáp án
* Hướng dẫn giải
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra : OH // IA // O’K
Theo giả thiết : IO = IO’
Suy ra : AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có : OH ⊥ AC
Suy ra : HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có : O’K ⊥ AD
Suy ra : KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 1 !!
Số câu hỏi: 814
Copyright © 2021 HOCTAP247